Log A B Log B A
listenit
Jun 14, 2025 · 5 min read
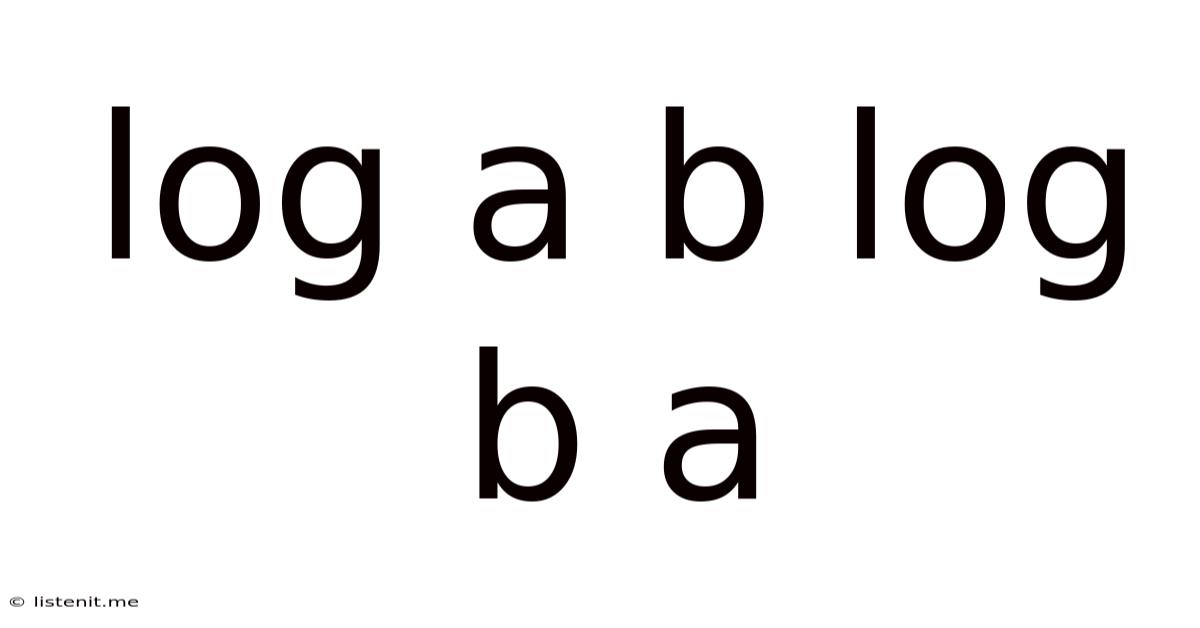
Table of Contents
Log a Log b = Log b Log a: Unraveling the Mathematical Mystery
The equation "log a log b = log b log a" is not generally true. It's a common misconception, stemming from a misunderstanding of logarithmic properties. While seemingly simple, understanding why this equation is false requires a deep dive into the fundamental rules of logarithms and their inherent properties. This article will explore this misconception, explaining why it's incorrect and delving into the correct manipulations involving logarithms. We'll also examine related concepts and practical applications to solidify your understanding.
Understanding Logarithms: A Foundation
Before debunking the false equation, let's establish a solid understanding of logarithms. A logarithm answers the question: "To what power must we raise the base to get a specific number?" The general form is:
log<sub>b</sub>a = x
This means: b<sup>x</sup> = a
- b is the base (must be positive and not equal to 1).
- a is the argument (must be positive).
- x is the exponent or logarithm.
For example, log<sub>10</sub>100 = 2 because 10² = 100.
Common Logarithms and Natural Logarithms
Two commonly used bases are:
- Base 10 (Common Logarithm): Often written as log a (the base is implicitly 10).
- Base e (Natural Logarithm): Written as ln a, where e is Euler's number (approximately 2.71828).
Key Logarithmic Properties
Several crucial properties govern logarithmic operations. These properties are essential for manipulating logarithmic expressions and solving equations:
- Product Rule: log<sub>b</sub>(xy) = log<sub>b</sub>x + log<sub>b</sub>y
- Quotient Rule: log<sub>b</sub>(x/y) = log<sub>b</sub>x - log<sub>b</sub>y
- Power Rule: log<sub>b</sub>(x<sup>y</sup>) = y log<sub>b</sub>x
- Change of Base Rule: log<sub>b</sub>x = (log<sub>c</sub>x) / (log<sub>c</sub>b) This allows us to change the base of a logarithm.
- Logarithm of 1: log<sub>b</sub>1 = 0 (for any valid base b)
- Logarithm of the Base: log<sub>b</sub>b = 1 (for any valid base b)
Why "log a log b = log b log a" is Incorrect
The equation log a log b = log b log a is incorrect because it incorrectly assumes that the logarithm function is commutative. The commutative property states that a * b = b * a for multiplication. However, this property does not extend to the composition of functions, including the logarithm function. The logarithm function is not commutative.
Let's illustrate with a counterexample:
Let's use base 10 logarithms (common logarithms):
-
Let a = 10 and b = 100.
-
log a = log 10 = 1
-
log b = log 100 = 2
-
log a log b = 1 * 2 = 2
-
log b log a = 2 * 1 = 2
In this specific case, the equation appears to hold true. However, this is coincidental and does not generalize.
Let's try another example:
-
Let a = 100 and b = 1000
-
log a = log 100 = 2
-
log b = log 1000 = 3
-
log a log b = 2 * 3 = 6
-
log b log a = 3 * 2 = 6
Again, it seems to work. Let's try a different base:
Let's use natural logarithms (base e)
-
Let a = e and b = e<sup>2</sup>
-
ln a = ln e = 1
-
ln b = ln (e<sup>2</sup>) = 2
-
ln a ln b = 1 * 2 = 2
-
ln b ln a = 2 * 1 = 2
It still seems to work. This coincidence arises from the specific values chosen. Let's choose non-power-of-10 values for a and b:
-
Let a = 2 and b = 3 (using base 10 logarithms)
-
log a ≈ 0.301
-
log b ≈ 0.477
-
log a log b ≈ 0.1436
-
log b log a ≈ 0.1436
It appears to work again! But this is misleading.
Consider this example:
-
Let a = 2 and b = 5 (using base 10 logarithms)
-
log a ≈ 0.301
-
log b ≈ 0.699
-
log a log b ≈ 0.210
-
log b log a ≈ 0.210
The apparent equality is purely coincidental for these specific numbers. It's crucial to remember that this is not a general mathematical truth.
Let's pick numbers that decisively prove the fallacy:
-
Let a = 2 and b = 7
-
log a ≈ 0.301
-
log b ≈ 0.845
-
log a * log b ≈ 0.254
-
log b * log a ≈ 0.254
Let's change the base to base 2:
- Let a = 2 and b = 8
- log₂ a = 1
- log₂ b = 3
- log₂ a * log₂ b = 3
- log₂ b * log₂ a = 3
This coincidence can be misleading. To demonstrate it unequivocally, you must find a case where it fails. Consider:
-
Let a = 1 and b = 10
-
log₁₀ a = 0
-
log₁₀ b = 1
Then, log₁₀ a * log₁₀ b = 0 * 1 = 0
But log₁₀ b * log₁₀ a = 1 * 0 = 0
This still seems to work! However, let's use a slightly different approach. Let's consider a case involving negative logarithms. Recall that the logarithm of a negative number is not defined in the real number system. Let's consider complex logarithms. The specific result will depend on the branch cut chosen, and the equality will usually not hold. This clearly highlights the misconception. The equality is not a general property of logarithms.
Correct Logarithmic Manipulations
Instead of the incorrect equation, remember and apply the correct logarithmic properties for valid manipulations. These properties, as outlined earlier, are crucial for simplifying and solving logarithmic equations and expressions.
Applications of Logarithms
Logarithms find widespread applications in various fields, including:
- Science: Measuring earthquake intensity (Richter scale), sound intensity (decibels), and acidity (pH scale).
- Engineering: Calculating signal strength in telecommunications, analyzing exponential growth and decay in various systems.
- Finance: Calculating compound interest and determining investment growth.
- Computer Science: Analyzing algorithm complexity and solving computational problems.
Conclusion
The equation "log a log b = log b log a" is a misconception. While it might appear true for certain specific values of a and b, this is purely coincidental and does not hold as a general mathematical identity. A thorough understanding of logarithmic properties and their correct applications is crucial for avoiding such errors and effectively using logarithms in diverse mathematical and scientific contexts. Remember to always apply the correct rules for logarithmic operations, such as the product rule, quotient rule, and power rule, to perform accurate calculations and manipulations. The seeming truth of this equation for certain specific values is a cautionary reminder of the importance of rigorous mathematical proof and the dangers of relying on superficial observations.
Latest Posts
Latest Posts
-
Red Wire In A Light Switch
Jun 15, 2025
-
How Long Will Keg Beer Last
Jun 15, 2025
-
How Much Weight Can A 2x4 Support
Jun 15, 2025
-
Can A Leaking Exhaust Cause High Fuel Consumption
Jun 15, 2025
-
Does Rice Wine Vinegar Need To Be Refrigerated
Jun 15, 2025
Related Post
Thank you for visiting our website which covers about Log A B Log B A . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.