Limit Of Sinx X As X Approaches 0
listenit
May 11, 2025 · 5 min read
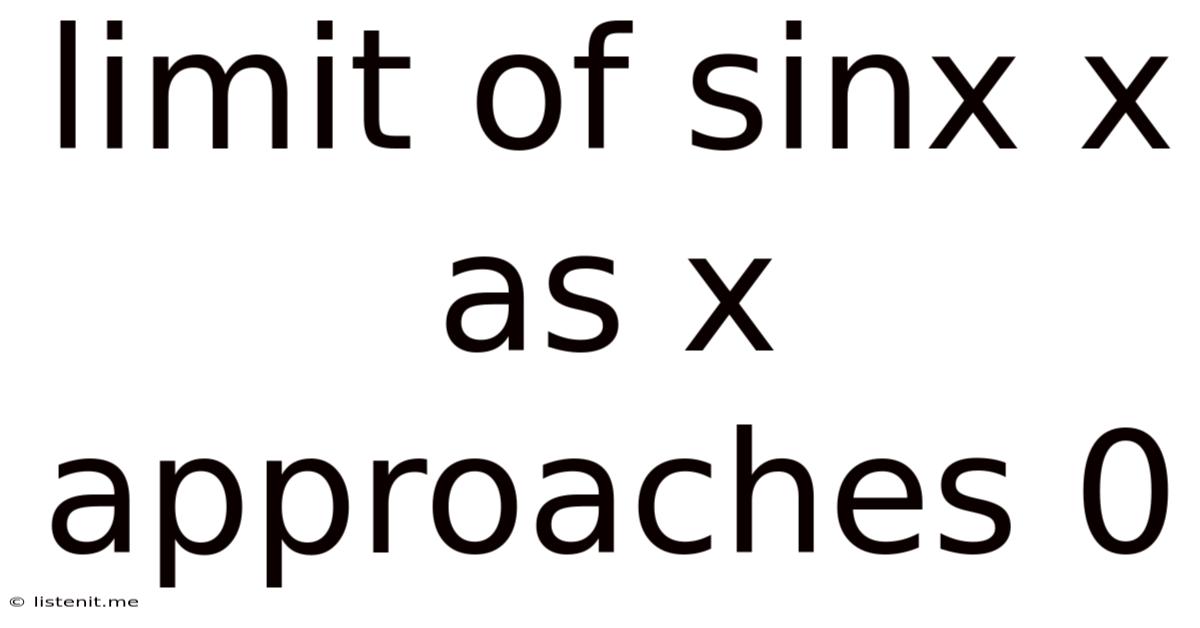
Table of Contents
The Limit of sin(x)/x as x Approaches 0: A Deep Dive
The limit of sin(x)/x as x approaches 0 is a fundamental concept in calculus, appearing frequently in various applications. Understanding this limit is crucial for grasping the intricacies of derivatives, integrals, and other advanced mathematical concepts. This comprehensive guide will delve into the proof of this limit, its applications, and its significance in the world of mathematics and beyond.
Understanding the Limit
Before we dive into the proof, let's understand what we're trying to find. The expression lim (x→0) sin(x)/x represents the value the function sin(x)/x approaches as x gets arbitrarily close to 0, but doesn't actually equal 0. Intuitively, you might think this limit is undefined because we'd be dividing by zero. However, a careful examination using techniques of calculus reveals a surprising and elegant result: the limit is 1.
The Geometric Proof: A Visual Approach
One of the most elegant ways to understand this limit is through a geometric proof. Consider a unit circle (a circle with radius 1). Let's define an angle x (in radians) in this circle. We can construct a right-angled triangle within the circle, with the hypotenuse as the radius (length 1), and one leg having a length of sin(x) and the other having length cos(x). We can also construct a sector of the circle with the same angle x.
Now, let's compare the areas:
- Area of triangle: (1/2) * sin(x) * cos(x)
- Area of sector: (1/2) * x * 1² = x/2
- Area of triangle with hypotenuse along tangent: (1/2) * tan(x) * 1 = tan(x)/2
We can now create inequalities based on the areas:
(1/2) * sin(x) * cos(x) < x/2 < (1/2) * tan(x)
Simplifying and focusing on the left and middle parts, we get:
sin(x) * cos(x) < x
Dividing by sin(x) (assuming x is not 0), we get:
cos(x) < x/sin(x)
Now, let's focus on the middle and right parts of the original inequality:
x/2 < (1/2) * tan(x)
This simplifies to:
x < tan(x) = sin(x)/cos(x)
Rearranging this inequality, we get:
cos(x) < sin(x)/x
Combining the inequalities, we have:
cos(x) < x/sin(x) and cos(x) < sin(x)/x
As x approaches 0, cos(x) approaches 1. Therefore, by the squeeze theorem (also known as the sandwich theorem), we can conclude that:
lim (x→0) sin(x)/x = 1
This geometric approach provides a strong intuitive understanding of why the limit is 1.
The Squeeze Theorem: Formalizing the Proof
The geometric approach provides intuition, but the squeeze theorem provides the rigorous mathematical proof. The squeeze theorem states that if we have three functions, f(x), g(x), and h(x), such that f(x) ≤ g(x) ≤ h(x) for all x near a point c (excluding c itself), and lim (x→c) f(x) = lim (x→c) h(x) = L, then lim (x→c) g(x) = L.
We already established the inequalities relating sin(x), x, and tan(x) in the geometric proof. Using these inequalities and the squeeze theorem, we formally prove the limit.
Remember, we derived the inequalities:
cos(x) < x/sin(x) and cos(x) < sin(x)/x
As x approaches 0, cos(x) approaches 1. Therefore, as x approaches 0, x/sin(x) and sin(x)/x both approach 1. This fulfills the conditions of the squeeze theorem, conclusively proving that:
lim (x→0) sin(x)/x = 1
Applications of the Limit
This seemingly simple limit has far-reaching consequences in various areas of mathematics and beyond:
1. Differentiation: Finding Derivatives
The derivative of a function at a point represents the instantaneous rate of change. The limit of sin(x)/x is fundamental in deriving the derivative of sin(x), which is cos(x). The proof involves the definition of the derivative using limits, and this particular limit is an essential step in that derivation.
2. L'Hôpital's Rule: Handling Indeterminate Forms
L'Hôpital's Rule is a powerful tool for evaluating limits of indeterminate forms (0/0, ∞/∞). Many applications of L'Hôpital's rule involve this limit directly or indirectly. Often, when applying L'Hôpital's rule, we encounter the derivative of sin(x), relying on the fundamental limit we've discussed.
3. Taylor and Maclaurin Series: Approximating Functions
Taylor and Maclaurin series are powerful tools for approximating functions using infinite sums of terms. The derivation of these series relies heavily on limits, and the limit of sin(x)/x plays a crucial role in the development of the Taylor series for trigonometric functions.
4. Physics and Engineering: Modeling Oscillations and Waves
In physics and engineering, the sine and cosine functions are used extensively to model oscillatory phenomena, such as simple harmonic motion, wave propagation, and alternating current circuits. The limit of sin(x)/x appears implicitly in these models, influencing the accuracy and interpretation of the results. For instance, understanding small angle approximations in simple harmonic motion relies directly on this limit.
Exploring Related Limits
Understanding the limit of sin(x)/x allows us to easily derive other related limits:
-
lim (x→0) (1 - cos(x))/x: This limit can be solved by manipulating the expression using trigonometric identities and the limit we've already established. The result is 0.
-
lim (x→0) sin(ax)/x: By a simple substitution and using the limit of sin(x)/x, this limit simplifies to 'a'.
-
lim (x→0) (1 - cos(x))/x²: Similar to the previous example, this limit requires some algebraic manipulation and the knowledge of the fundamental limit. The result is 1/2.
Conclusion: The Significance of a Fundamental Limit
The limit of sin(x)/x as x approaches 0 is far more than just a mathematical curiosity. It's a cornerstone of calculus, serving as a fundamental building block for numerous applications. Its elegance and importance lie not only in its simple result but also in its profound implications across various fields, from theoretical mathematics to practical engineering applications. By understanding its derivation and applications, we gain a deeper appreciation for the power and beauty of calculus. Mastering this limit unlocks a deeper understanding of many advanced mathematical concepts and their real-world applications. The intuitive geometric approach combined with the rigorous proof using the squeeze theorem provides a solid foundation for anyone seeking a thorough understanding of this crucial mathematical concept.
Latest Posts
Latest Posts
-
Why Do Electric Field Lines Never Cross
May 13, 2025
-
1 10 As A Percent And Decimal
May 13, 2025
-
Can All Minerals Be A Gemstone
May 13, 2025
-
Multicellular Heterotrophs Without A Cell Wall
May 13, 2025
-
What Are The Gcf Of 48
May 13, 2025
Related Post
Thank you for visiting our website which covers about Limit Of Sinx X As X Approaches 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.