Lim Of Sinx X As X Approaches 0
listenit
May 11, 2025 · 5 min read
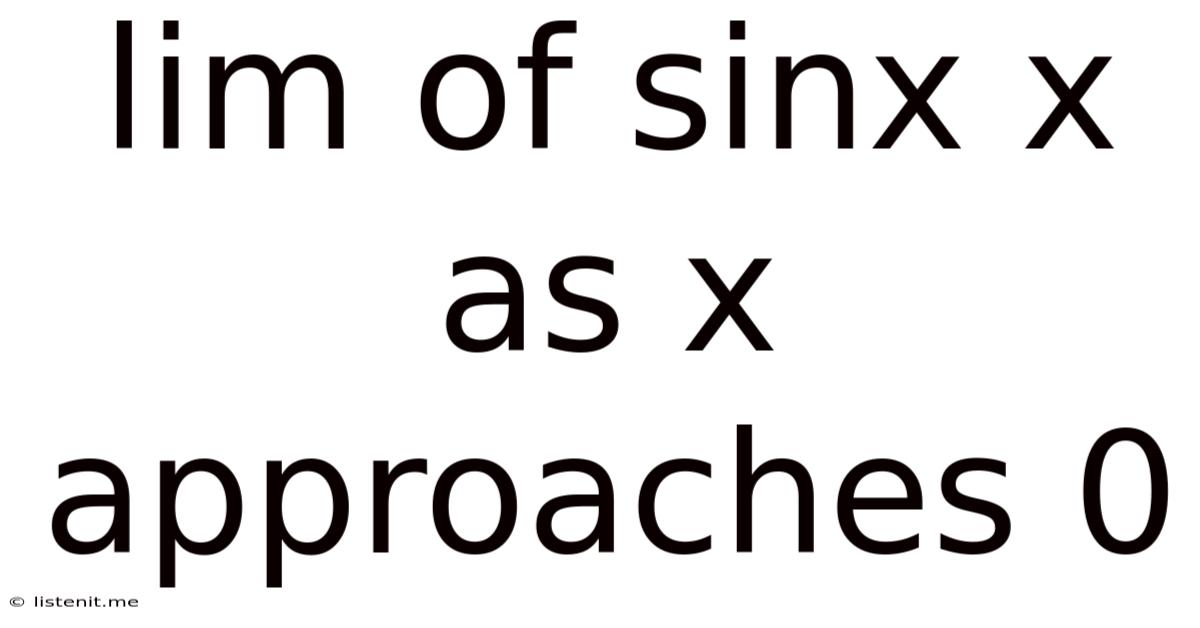
Table of Contents
The Limit of sin(x)/x as x Approaches 0: A Deep Dive
The limit of sin(x)/x as x approaches 0 is a fundamental concept in calculus, with far-reaching implications across mathematics, physics, and engineering. Understanding this limit is crucial for grasping concepts like derivatives, integrals, and Taylor series. This article will explore this limit in detail, examining its proof, applications, and significance.
Understanding the Limit
Before diving into the proof, let's establish a clear understanding of what we're trying to determine:
lim (x→0) sin(x)/x
This expression asks: "What value does the ratio sin(x)/x approach as x gets infinitely close to 0?" Intuitively, it might seem like we'd get 0/0, an indeterminate form. However, this is where the beauty of calculus comes into play. We're not interested in the value at x=0 (which is undefined), but rather the value the function approaches as x gets arbitrarily close to 0.
The Geometric Proof
One of the most elegant ways to prove this limit is through geometric reasoning. Consider a unit circle (radius = 1). Let's draw a right-angled triangle within this circle, with angle x at the center. The opposite side of this triangle has length sin(x), and the arc length subtended by the angle x is also x (because we're dealing with a unit circle).
Now, consider another triangle created by extending the opposite side to intersect with the circle's tangent at a point. This forms a larger triangle where the opposite side's length is tan(x).
We now have three quantities:
- sin(x): The length of the opposite side of the smaller triangle.
- x: The arc length.
- tan(x): The length of the opposite side of the larger triangle.
By comparing the areas of these triangles and the sector, we can establish inequalities:
sin(x) < x < tan(x)
Dividing by sin(x) (since sin(x) > 0 for small positive x), we get:
1 < x/sin(x) < 1/cos(x)
Taking reciprocals and reversing the inequalities, we get:
cos(x) < sin(x)/x < 1
As x approaches 0, cos(x) approaches 1. By the Squeeze Theorem (also known as the Sandwich Theorem), since both the lower and upper bounds approach 1 as x approaches 0, the limit of sin(x)/x must also be 1.
Therefore: lim (x→0) sin(x)/x = 1
The Taylor Series Approach
Another powerful method to demonstrate this limit involves using Taylor series expansions. The Taylor series expansion for sin(x) around x = 0 is:
sin(x) = x - x³/3! + x⁵/5! - x⁷/7! + ...
Dividing by x, we get:
sin(x)/x = 1 - x²/3! + x⁴/5! - x⁶/7! + ...
As x approaches 0, all the terms with x in them approach 0, leaving us with:
lim (x→0) sin(x)/x = 1
Significance and Applications
The seemingly simple result – lim (x→0) sin(x)/x = 1 – has profound consequences throughout mathematics and its applications:
1. Derivative of sin(x):
The derivative of sin(x) is defined as:
d(sin(x))/dx = lim (h→0) [sin(x+h) - sin(x)]/h
Using trigonometric identities and the limit we've established, this simplifies to cos(x). This foundational derivative is essential for countless applications in physics and engineering.
2. L'Hôpital's Rule:
L'Hôpital's Rule is a powerful technique for evaluating indeterminate forms like 0/0 or ∞/∞. The limit of sin(x)/x often serves as a crucial example and building block in understanding and applying L'Hôpital's Rule.
3. Fourier Analysis:
Fourier analysis decomposes complex functions into simpler sinusoidal components. The limit of sin(x)/x plays a key role in the derivation and understanding of Fourier transforms, which are fundamental in signal processing, image processing, and other areas.
4. Physics and Engineering:
This limit appears frequently in the study of oscillations, wave phenomena, and other physical systems where sinusoidal functions are involved. Examples include:
- Simple Harmonic Motion: The analysis of pendulums and springs often involves the limit of sin(x)/x for small angles.
- Wave Propagation: The study of waves (light, sound, etc.) uses sinusoidal functions extensively, and the limit is crucial for simplifying calculations in many cases.
- Optics: Diffraction and interference phenomena in optics rely on the properties of sine waves, and understanding this limit is vital for calculations.
5. Probability and Statistics:
In probability theory, certain distributions (like the normal distribution) are defined using integrals that involve trigonometric functions. The limit of sin(x)/x helps in the evaluation of these integrals.
Addressing Common Misconceptions
It's important to clarify some common misunderstandings regarding this limit:
-
It's not about plugging in x=0: Remember, we're dealing with a limit, not direct substitution. Plugging in x=0 leads to the indeterminate form 0/0, which is meaningless.
-
The limit is about the behavior near 0, not at 0: The crucial aspect is how the function approaches a value as x gets incredibly close to 0.
-
Units matter: In real-world applications, the angle x must be expressed in radians, not degrees. This is because the derivation of the limit relies on the geometrical interpretation where x represents arc length on the unit circle, which is inherently a radian measure.
Conclusion
The limit of sin(x)/x as x approaches 0 is a cornerstone of calculus and has profound implications across various fields. Understanding its proof, significance, and applications is crucial for anyone pursuing a deeper understanding of mathematics, physics, or engineering. Its seemingly simple result underpins much of the more complex mathematical machinery we use to model and understand the world around us. The multiple approaches to proving this limit highlight the rich interconnectivity of different mathematical concepts and their power in solving problems. The limit itself stands as a testament to the elegance and power of mathematical reasoning.
Latest Posts
Latest Posts
-
A Car Travels Up A Hill At A Constant Speed
May 11, 2025
-
The Slope Of A Velocity Time Graph Represents
May 11, 2025
-
How To Find The Charge Of A Transition Metal
May 11, 2025
-
Binary Molecular Compounds Are Made Of Two
May 11, 2025
-
7 2 Cm Is How Many Inches
May 11, 2025
Related Post
Thank you for visiting our website which covers about Lim Of Sinx X As X Approaches 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.