Lim 1 X As X Approaches Infinity
listenit
May 09, 2025 · 6 min read
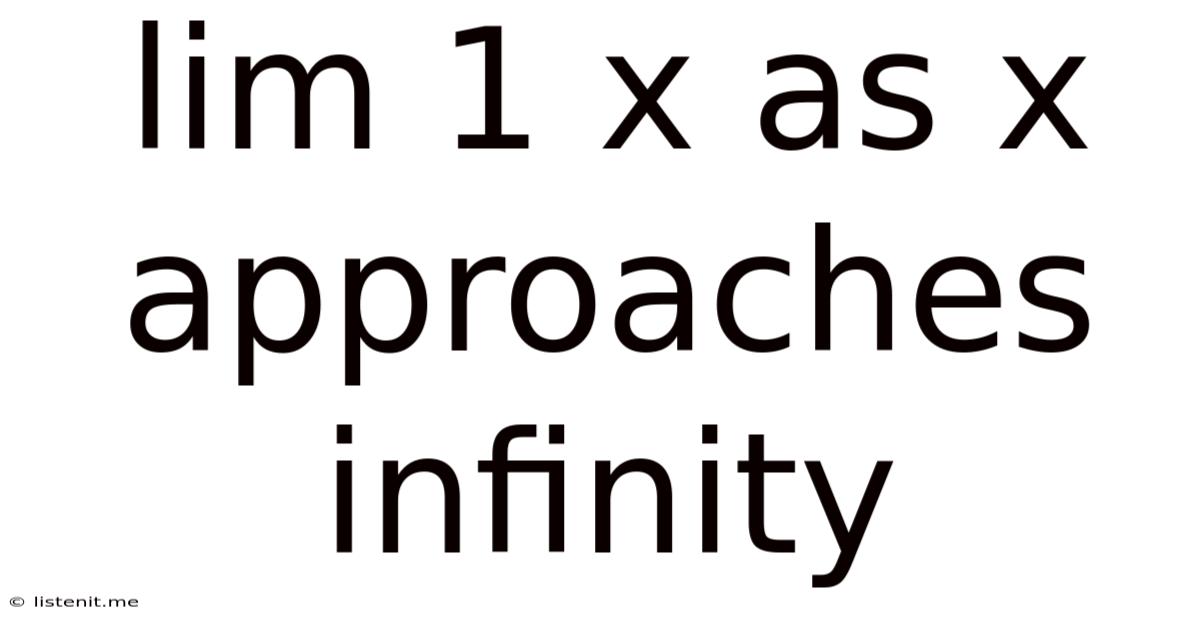
Table of Contents
Understanding the Limit of 1/x as x Approaches Infinity
The concept of limits is fundamental to calculus and real analysis. Understanding how functions behave as their input values approach certain points, particularly infinity, is crucial for grasping many mathematical concepts. This article delves into the limit of the function f(x) = 1/x as x approaches infinity, exploring its meaning, implications, and applications. We'll also touch upon related concepts and provide practical examples.
What is a Limit?
Before diving into the specific limit of 1/x, let's establish a clear understanding of what a limit is. Informally, the limit of a function f(x) as x approaches a value 'a' (denoted as lim_(x→a) f(x)) is the value that f(x) gets arbitrarily close to as x gets arbitrarily close to 'a'. Crucially, x doesn't actually have to equal 'a'; the limit describes the function's behavior near 'a'.
This becomes particularly interesting when considering limits as x approaches infinity (∞). In this case, we're interested in the behavior of the function as x grows without bound. The function doesn't need to ever actually reach infinity; we're examining its trend as x increases indefinitely.
Evaluating lim_(x→∞) 1/x
Now, let's consider the specific function f(x) = 1/x. As x becomes increasingly large (approaches infinity), the value of 1/x becomes increasingly small. Consider a few examples:
- If x = 10, then 1/x = 0.1
- If x = 100, then 1/x = 0.01
- If x = 1000, then 1/x = 0.001
- If x = 1,000,000, then 1/x = 0.000001
As you can see, as x grows larger and larger, 1/x gets closer and closer to zero. We can express this mathematically as:
lim_(x→∞) 1/x = 0
This means that the limit of the function 1/x as x approaches infinity is 0. No matter how large x becomes, 1/x will always be a positive number, but it will approach zero as a limit. This is a fundamental concept in many areas of mathematics and science.
Graphical Representation
Visualizing this limit graphically can enhance understanding. The graph of y = 1/x is a hyperbola. As x increases along the positive x-axis, the curve approaches the x-axis (y = 0) asymptotically. This asymptotic behavior clearly demonstrates that the function's value approaches zero as x approaches infinity. Similarly, as x approaches negative infinity, the function approaches zero from the negative side.
Formal Definition of a Limit (Epsilon-Delta Approach)
For a more rigorous understanding, we can use the epsilon-delta definition of a limit. For any ε > 0, there exists an M > 0 such that if x > M, then |1/x - 0| < ε. This formally states that we can make 1/x arbitrarily close to 0 (within ε) by choosing a sufficiently large x (greater than M). This is a formal proof of the limit.
Applications of the Limit
The limit lim_(x→∞) 1/x = 0 has widespread applications in various fields:
1. Calculus and Analysis:
- Infinite Series: Understanding this limit is crucial for analyzing the convergence of infinite series. Many tests for convergence rely on the behavior of terms as the index approaches infinity.
- Limits of Sequences: Sequences of numbers can be analyzed using limits, and this limit often appears in determining the convergence of sequences.
- Asymptotic Analysis: This limit is fundamental in analyzing the asymptotic behavior of functions. Asymptotic analysis helps us understand how functions behave as their inputs become very large or very small.
2. Physics and Engineering:
- Decaying Processes: Many physical phenomena, such as radioactive decay or the cooling of an object, involve exponential decay. The limit helps to analyze the long-term behavior of these processes.
- Probability and Statistics: In probability theory, the limit of probabilities often involves expressions where this limit plays a role.
- Fluid Dynamics: Modeling fluid behavior often involves asymptotic analysis, using the limit to understand the behavior of fluid flow in certain conditions.
3. Computer Science:
- Algorithm Analysis: The efficiency of algorithms is often analyzed using Big O notation, which involves comparing the growth rate of functions as the input size approaches infinity. This limit forms the base for such comparisons.
- Numerical Analysis: Approximating solutions to problems often involves iterative methods that converge to a solution. Understanding limits helps in analyzing the convergence behavior of these methods.
Related Limits and Concepts
Understanding the limit of 1/x as x approaches infinity provides a foundation for understanding related limits and concepts:
- lim_(x→∞) 1/x^n = 0 (for n > 0): Generalizing the limit, we see that the limit of 1/x raised to any positive power also approaches 0 as x approaches infinity.
- lim_(x→0) 1/x: This limit does not exist. As x approaches 0 from the positive side, 1/x approaches positive infinity, and as x approaches 0 from the negative side, 1/x approaches negative infinity. The limit only exists if the function approaches the same value from both sides.
- L'Hôpital's Rule: While not directly applicable in this simple case, L'Hôpital's Rule is a powerful technique for evaluating limits of indeterminate forms, such as 0/0 or ∞/∞, which arise frequently in more complex scenarios.
Practical Examples
Let's look at a couple of practical examples illustrating the application of this limit:
Example 1: Cooling of an Object:
Imagine an object cooling down in a room. Newton's Law of Cooling states that the rate of cooling is proportional to the temperature difference between the object and its surroundings. The temperature difference decreases over time, and the rate of cooling approaches zero as the object approaches room temperature. This behavior is described mathematically using a limit that incorporates 1/x, representing the diminishing rate of change.
Example 2: Probability of an Event:
Consider the probability of getting heads when flipping a fair coin repeatedly. While the probability of getting heads on any single flip is 0.5, the probability of getting heads on every flip in a sequence of an increasingly large number of flips approaches zero. This illustrates the limit as the number of flips approaches infinity.
Conclusion
The seemingly simple limit of 1/x as x approaches infinity, while straightforward in its calculation, holds significant importance in numerous areas of mathematics, science, and engineering. Understanding this limit is not only crucial for mastering calculus but also for comprehending the behavior of various functions, processes, and phenomena. Its application ranges from analyzing the convergence of infinite series and asymptotic behavior of functions to modeling real-world phenomena involving decay, probability, and algorithm efficiency. The thorough understanding of this limit paves the way for tackling more complex limit problems and deeper mathematical concepts. Its fundamental nature underscores its enduring significance in mathematical analysis and its practical applications in various disciplines.
Latest Posts
Latest Posts
-
7 Minus The Product Of 3 And X
May 10, 2025
-
Granulation Is Evidence Of What Phenomenon
May 10, 2025
-
How Many Electrons Can The 5th Shell Hold
May 10, 2025
-
Graph The Line 2x Y 4
May 10, 2025
-
Can Both Liquid Water And Steam Exist At 100 C
May 10, 2025
Related Post
Thank you for visiting our website which covers about Lim 1 X As X Approaches Infinity . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.