Is The Median Of A Trapezoid Parallel To Eahc Base
listenit
Apr 04, 2025 · 4 min read
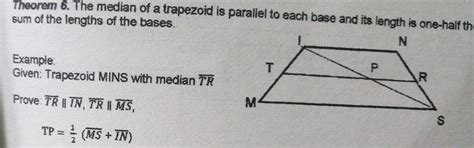
Table of Contents
Is the Median of a Trapezoid Parallel to Each Base? A Comprehensive Exploration
The question of whether the median of a trapezoid is parallel to its bases is a fundamental concept in geometry. The answer, unequivocally, is yes. This article will delve deep into proving this statement, exploring related theorems, and providing practical applications and examples to solidify your understanding. We’ll also discuss related concepts and tackle some common misconceptions.
Understanding the Median of a Trapezoid
Before diving into the proof, let's define our terms. A trapezoid (or trapezium in some regions) is a quadrilateral with at least one pair of parallel sides. These parallel sides are called the bases of the trapezoid. The median of a trapezoid is the line segment connecting the midpoints of the two non-parallel sides (legs) of the trapezoid.
Let's consider a trapezoid ABCD, where AB is parallel to CD. Let M be the midpoint of AD and N be the midpoint of BC. The line segment MN is the median of trapezoid ABCD. Our goal is to prove that MN is parallel to both AB and CD.
Proof: The Median of a Trapezoid is Parallel to the Bases
We will use a vector approach to prove this, but several other methods exist (coordinate geometry, synthetic geometry). The vector approach offers a concise and elegant solution.
1. Defining Vectors:
Let's represent the vertices of the trapezoid using vectors:
- A represents the vector from the origin to point A.
- B represents the vector from the origin to point B.
- C represents the vector from the origin to point C.
- D represents the vector from the origin to point D.
2. Midpoint Vectors:
The midpoint M of AD is given by the vector:
M = (A + D) / 2
Similarly, the midpoint N of BC is given by:
N = (B + C) / 2
3. Vector Representing the Median:
The vector representing the median MN is given by the difference between the vectors representing points N and M:
MN = N - M = (B + C) / 2 - (A + D) / 2 = (B + C - A - D) / 2
4. Utilizing the Parallel Condition:
Since AB is parallel to CD, we can express the vector representing CD as a scalar multiple of the vector representing AB. Let's say:
CD = C - D = k(B - A) where 'k' is a scalar.
5. Rewriting the Median Vector:
Now, let's manipulate the median vector:
MN = (B + C - A - D) / 2 = (B - A + C - D) / 2
Substituting the expression for C - D from step 4:
MN = (B - A + k(B - A)) / 2 = (1 + k)(B - A) / 2
6. Conclusion:
Notice that the vector MN is a scalar multiple of the vector AB (specifically, [(1+k)/2] * AB). This conclusively proves that MN is parallel to AB. A similar argument can be used to show that MN is parallel to CD. Therefore, the median of a trapezoid is parallel to both bases.
Length of the Median: An Important Corollary
Another significant property of the trapezoid median is its length. The length of the median is the average of the lengths of the bases. Mathematically:
MN = (AB + CD) / 2
This can be derived using the same vector approach or through other geometric methods. This property is extremely useful in various problem-solving scenarios involving trapezoids.
Applications and Examples
The properties of the trapezoid median find applications in various fields, including:
- Civil Engineering: Calculating the load distribution in structural elements shaped like trapezoids.
- Architecture: Designing roof structures and other architectural elements.
- Computer Graphics: Creating and manipulating trapezoidal shapes in computer-aided design (CAD) software.
- Calculus: Calculating areas using trapezoidal rule approximation.
Example Problem:
Let's say we have a trapezoid with bases of length 6 cm and 10 cm. What is the length of its median?
Using the formula: MN = (AB + CD) / 2 = (6 + 10) / 2 = 8 cm. The median of the trapezoid is 8 cm long.
Common Misconceptions
A common misconception is that the median bisects the area of the trapezoid. While the median is parallel to the bases, it does not, in general, bisect the area. The area is only bisected if the trapezoid is an isosceles trapezoid (a trapezoid with equal legs).
Related Theorems and Concepts
Understanding the median of a trapezoid is closely linked to other geometric concepts:
- Midpoint Theorem: The midpoint theorem states that the line segment connecting the midpoints of two sides of a triangle is parallel to the third side and half its length. The proof of the trapezoid median's properties often leverages the midpoint theorem.
- Similar Triangles: Constructing similar triangles within a trapezoid often aids in proving properties of the median.
- Vectors in Geometry: As demonstrated above, vectors provide a powerful and elegant tool for proving geometric theorems.
Conclusion
The median of a trapezoid is a crucial element in understanding the geometry of this quadrilateral. Its parallelism to the bases and the relationship between its length and the lengths of the bases are fundamental properties with significant practical applications. This comprehensive exploration has covered the proof, practical implications, related concepts, and addressed common misconceptions. Understanding these properties provides a solid foundation for further exploration into geometric concepts. By mastering the properties of the trapezoid median, you unlock a deeper understanding of geometry and its applications in various fields.
Latest Posts
Latest Posts
-
What Is The Decimal For 17 20
Apr 04, 2025
-
What Is The Name Of The Compound Ca No3 2
Apr 04, 2025
-
What Is The Percent Acetic Acid In Vinegar
Apr 04, 2025
-
What Type Of Elements Are Involved In Covalent Bonding
Apr 04, 2025
-
Miles Per Hour To Meters Per Hour
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Is The Median Of A Trapezoid Parallel To Eahc Base . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
