Is Soh Cah Toa Only For Right Triangles
listenit
Apr 03, 2025 · 5 min read
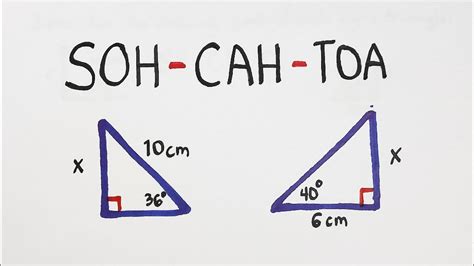
Table of Contents
Is SOH CAH TOA Only for Right Triangles?
The mnemonic SOH CAH TOA is a cornerstone of trigonometry education, helping students remember the fundamental relationships between angles and sides in right-angled triangles. But the question often arises: is SOH CAH TOA only applicable to right triangles? The short answer is yes, in its simplest, most directly applicable form. However, the underlying concepts extend far beyond right triangles, offering a gateway to a broader understanding of trigonometry. This article delves deep into the intricacies of SOH CAH TOA, exploring its limitations and demonstrating how its principles form the foundation for solving problems involving all types of triangles, and even beyond.
Understanding SOH CAH TOA in Right-Angled Triangles
Let's begin with a firm grasp of SOH CAH TOA in its familiar context:
- SOH: Sine (sin) = Opposite / Hypotenuse
- CAH: Cosine (cos) = Adjacent / Hypotenuse
- TOA: Tangent (tan) = Opposite / Adjacent
These ratios relate the lengths of the sides of a right-angled triangle to the angles within it. The "hypotenuse" is always the side opposite the right angle; the "opposite" side is opposite the angle being considered; and the "adjacent" side is next to the angle being considered, and not the hypotenuse. This straightforward application makes SOH CAH TOA incredibly useful for solving many practical problems involving right triangles – from calculating the height of a building given an angle of elevation to determining the distance across a river using triangulation.
Examples of SOH CAH TOA in Right-Angled Triangles
Consider a right-angled triangle with a hypotenuse of 10 units and one angle of 30 degrees. Using SOH CAH TOA:
- Finding the Opposite side: sin(30°) = Opposite / 10 => Opposite = 10 * sin(30°) = 5 units
- Finding the Adjacent side: cos(30°) = Adjacent / 10 => Adjacent = 10 * cos(30°) = 8.66 units (approximately)
These calculations highlight the direct and straightforward application of SOH CAH TOA in the context of right-angled triangles. The simplicity and effectiveness of this method make it an indispensable tool for many geometric problems.
Extending Beyond Right Triangles: The Sine Rule and Cosine Rule
While SOH CAH TOA directly applies only to right-angled triangles, the underlying principles of trigonometric ratios are crucial for solving problems involving any triangle. This is achieved through the Sine Rule and the Cosine Rule.
The Sine Rule
The Sine Rule states:
a / sin(A) = b / sin(B) = c / sin(C)
where 'a', 'b', and 'c' are the lengths of the sides opposite angles A, B, and C respectively. This rule is particularly useful when you know:
- Two angles and one side (AAS or ASA)
- Two sides and one non-included angle (SSA - ambiguous case)
The Cosine Rule
The Cosine Rule states:
a² = b² + c² - 2bc * cos(A)
This rule can be rearranged to solve for any side or angle in a triangle, given sufficient information. It's particularly useful when you know:
- Three sides (SSS)
- Two sides and the included angle (SAS)
Examples of Sine and Cosine Rule Applications
Imagine a triangle with sides a = 5, b = 7, and angle C = 60°. To find side 'c', we would use the Cosine Rule:
c² = 5² + 7² - 2 * 5 * 7 * cos(60°) c² = 25 + 49 - 35 c² = 39 c = √39 ≈ 6.24
This demonstrates how the Cosine Rule allows us to solve for missing sides in non-right-angled triangles, leveraging principles related to the trigonometric ratios within the SOH CAH TOA framework.
The Unit Circle and Beyond: A Deeper Understanding of Trigonometric Functions
To truly grasp the universality of the trigonometric functions, we need to move beyond the confines of triangles and consider the unit circle. The unit circle is a circle with a radius of 1 unit centered at the origin of a coordinate plane. Each point on the unit circle can be defined by an angle (θ) and its corresponding x and y coordinates. These coordinates are directly related to the cosine and sine functions:
- x = cos(θ)
- y = sin(θ)
This representation shows that sine and cosine are not just ratios of sides in triangles but functions of angles with broader application in fields like wave mechanics, oscillations, and circular motion. The tangent function, similarly, can be defined as the slope of the line connecting the origin to a point on the unit circle.
The unit circle representation extends the domain of trigonometric functions beyond the acute angles found in right-angled triangles. We can now meaningfully talk about sine, cosine, and tangent of angles greater than 90 degrees, negative angles, and even angles beyond 360 degrees (representing multiple rotations).
Applications in other fields
Beyond its obvious use in geometry and surveying, the extended reach of trigonometry has a profound impact on various fields. Some examples include:
- Physics: Modeling oscillations (like pendulums or springs), wave phenomena (sound and light), projectile motion, and rotational dynamics.
- Engineering: Calculating forces and stresses in structures, designing mechanisms, and analyzing vibrations.
- Computer Graphics: Transforming and rotating objects in 2D and 3D space.
- Signal Processing: Analyzing and manipulating audio, video, and other signals.
Advanced Trigonometric Identities and their relationship to SOH CAH TOA
SOH CAH TOA, while limited to right triangles in its basic form, provides the foundational understanding for more complex trigonometric identities. These identities are powerful tools for simplifying expressions, solving equations, and proving more intricate geometric relationships.
Some key identities derived from the fundamental ratios include:
- Pythagorean Identity: sin²(θ) + cos²(θ) = 1 (Directly derived from the Pythagorean theorem in a right-angled triangle)
- Tangent Identity: tan(θ) = sin(θ) / cos(θ) (Directly derived from SOH CAH TOA)
- Reciprocal Identities: sec(θ) = 1/cos(θ), csc(θ) = 1/sin(θ), cot(θ) = 1/tan(θ)
These and other more complex identities allow for the manipulation and simplification of trigonometric expressions, offering powerful techniques to solve problems that initially seem intractable.
Conclusion: SOH CAH TOA's Legacy
While the mnemonic SOH CAH TOA directly applies only to right-angled triangles, it acts as the seed from which a much wider understanding of trigonometry grows. The fundamental trigonometric ratios it represents are the foundation for the Sine Rule, the Cosine Rule, and countless other identities that extend the reach of trigonometry far beyond the realm of right-angled triangles. The unit circle representation provides a visual and conceptual framework that further elucidates the scope of these functions, showcasing their relevance in numerous scientific and engineering applications. Thus, while SOH CAH TOA itself is limited, its underlying concepts are fundamental and far-reaching, forming a critical building block for mastering the broader world of trigonometry. The simple mnemonic serves as a powerful starting point for understanding a subject rich in complexity and applications.
Latest Posts
Latest Posts
-
Lowest Common Multiple Of 2 3 And 7
Apr 03, 2025
-
What Is The Decimal Of 8 9
Apr 03, 2025
-
How Are Heat And Temperature Related
Apr 03, 2025
-
37 1 2 As A Fraction
Apr 03, 2025
-
How Many Ounes In A Pound
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Is Soh Cah Toa Only For Right Triangles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
