Is An Isosceles Trapezoid A Parallelogram
listenit
Apr 07, 2025 · 5 min read
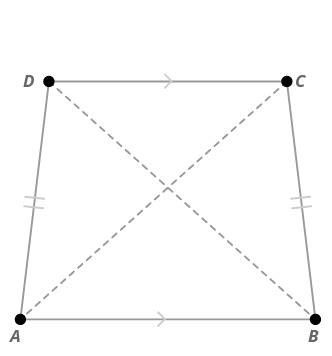
Table of Contents
Is an Isosceles Trapezoid a Parallelogram? A Deep Dive into Quadrilateral Properties
The question of whether an isosceles trapezoid is a parallelogram is a fundamental one in geometry, often causing confusion among students. The short answer is no, an isosceles trapezoid is not a parallelogram. However, understanding why requires a thorough examination of the defining properties of both shapes. This article will delve into the characteristics of parallelograms and isosceles trapezoids, highlighting their similarities and crucial differences. We'll explore the geometric proofs and demonstrate why the two quadrilaterals are distinct despite sharing some common features.
Understanding Parallelograms
A parallelogram is a quadrilateral with two pairs of parallel sides. This defining characteristic leads to several other properties:
- Opposite sides are parallel and congruent: This is the fundamental property. If AB is parallel to CD, and BC is parallel to AD, then AB = CD and BC = AD.
- Opposite angles are congruent: Angle A is congruent to Angle C, and Angle B is congruent to Angle D.
- Consecutive angles are supplementary: The sum of any two consecutive angles (e.g., Angle A + Angle B) equals 180 degrees.
- Diagonals bisect each other: The diagonals of a parallelogram intersect at a point that divides each diagonal into two equal segments.
These properties are interconnected and can be proven using basic geometric postulates and theorems. The parallel sides are the cornerstone of all other properties.
Delving into Isosceles Trapezoids
An isosceles trapezoid is a quadrilateral with only one pair of parallel sides (the bases) and the non-parallel sides (legs) are congruent. This is the defining characteristic that distinguishes it from other trapezoids and parallelograms. Let's break down its properties:
- One pair of parallel sides: This is the essential property. Let's say AB is parallel to CD.
- Non-parallel sides are congruent: The lengths of AD and BC are equal (AD = BC).
- Base angles are congruent: The angles adjacent to each base are congruent. This means Angle A is congruent to Angle B, and Angle C is congruent to Angle D. This is a crucial difference from a general trapezoid.
- Diagonals are congruent: The diagonals AC and BD have the same length (AC = BD). This is another unique characteristic differentiating it from a general trapezoid.
Note that while an isosceles trapezoid possesses some similarities to a parallelogram (e.g., congruent base angles), it fundamentally lacks the two pairs of parallel sides that define a parallelogram. This lack of parallel sides invalidates several properties unique to parallelograms, such as opposite sides being congruent and diagonals bisecting each other.
Why an Isosceles Trapezoid is NOT a Parallelogram: A Proof by Contradiction
To definitively demonstrate that an isosceles trapezoid isn't a parallelogram, we can employ a proof by contradiction. Let's assume, for the sake of contradiction, that an isosceles trapezoid is a parallelogram.
Assumption: Let's assume ABCD is an isosceles trapezoid where AB || CD (AB is parallel to CD) and AD = BC. We assume, contrary to the statement we want to prove, that ABCD is also a parallelogram.
Consequences of the Assumption: If ABCD were a parallelogram, then by definition, AD || BC (AD is parallel to BC). This implies that both pairs of opposite sides are parallel.
Contradiction: However, we initially defined ABCD as an isosceles trapezoid, meaning only one pair of sides (AB and CD) are parallel. The condition AD || BC directly contradicts the definition of an isosceles trapezoid.
Conclusion: Because our assumption leads to a contradiction, the initial assumption that an isosceles trapezoid is a parallelogram must be false. Therefore, an isosceles trapezoid is not a parallelogram.
Visualizing the Difference: A Geometric Construction
Imagine constructing an isosceles trapezoid. Start by drawing two parallel lines representing the bases. Now, construct the congruent legs. Notice that the non-parallel sides will never be parallel; they will meet at some point if extended. This visual representation clearly showcases the key difference – the lack of a second pair of parallel sides, which is the defining characteristic of a parallelogram.
Exploring Special Cases and Related Concepts
While an isosceles trapezoid is not a parallelogram, it shares some properties with other quadrilaterals. Understanding these relationships can further clarify its unique place in geometry:
Isosceles Trapezoid vs. General Trapezoid
A general trapezoid only guarantees one pair of parallel sides. An isosceles trapezoid is a special case of a trapezoid with the added condition of congruent legs. The properties of congruent base angles and congruent diagonals are unique to isosceles trapezoids.
Isosceles Trapezoid and Cyclic Quadrilaterals
An isosceles trapezoid is a cyclic quadrilateral, meaning all its vertices lie on a single circle. This property stems directly from the congruent base angles. This connection links the isosceles trapezoid to a broader class of quadrilaterals with specific geometric constraints.
Isosceles Trapezoid and its Area
The area of an isosceles trapezoid, like any trapezoid, is given by the formula: Area = (1/2) * (sum of parallel sides) * height. The height is the perpendicular distance between the parallel bases. This formula applies regardless of the congruence of the legs.
Applications and Real-World Examples
Understanding the properties of isosceles trapezoids is essential in various fields:
- Architecture and Construction: The shape appears in building designs, bridge structures, and architectural elements.
- Engineering: Understanding its stability and structural properties is crucial in designing load-bearing structures.
- Computer Graphics: Isosceles trapezoids and other geometric shapes form the basis of many 2D and 3D models.
Conclusion: A Clear Distinction
In summary, although an isosceles trapezoid shares some superficial similarities with a parallelogram, it fundamentally lacks the crucial defining characteristic: two pairs of parallel sides. This lack of parallel sides invalidates the properties that define parallelograms. Understanding the distinct properties of both shapes—parallelograms and isosceles trapezoids—is critical for a thorough grasp of geometric principles and their applications in various fields. The proof by contradiction and visual representations clearly demonstrate why an isosceles trapezoid is distinctly different from and not a type of parallelogram.
Latest Posts
Latest Posts
-
A Word That Describes Or Modifies A Noun
Apr 07, 2025
-
What Stores Food And Water In A Cell
Apr 07, 2025
-
Write 9 10 As A Decimal Number
Apr 07, 2025
-
The Function Of A Buffer Is To
Apr 07, 2025
-
How Many Core Electrons Does Sulfur Have
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Is An Isosceles Trapezoid A Parallelogram . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.