Is 1 4 Equivalent To 3 12
listenit
May 11, 2025 · 5 min read
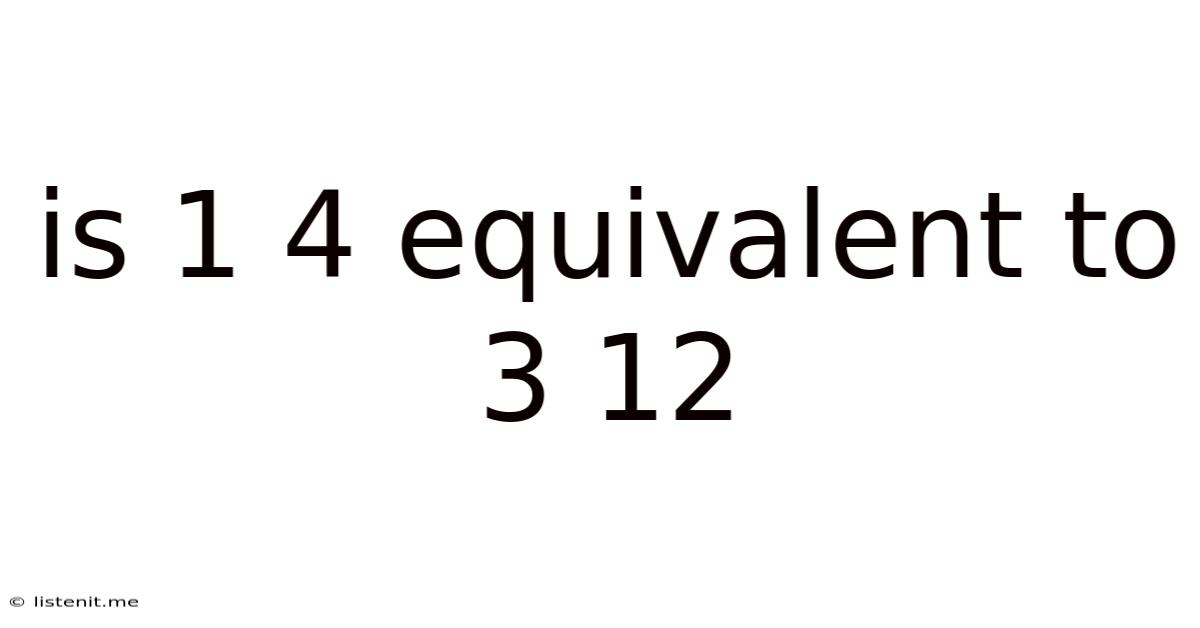
Table of Contents
Is 1/4 Equivalent to 3/12? A Deep Dive into Fraction Equivalence
The question, "Is 1/4 equivalent to 3/12?" might seem simple at first glance. For elementary school students just learning fractions, it might appear straightforward. However, a deeper understanding of fraction equivalence unlocks valuable insights into mathematical principles and lays the foundation for more complex algebraic concepts. This article will not only answer the question definitively but also explore the underlying mathematical concepts, providing practical examples and demonstrating why understanding fraction equivalence is crucial.
Understanding Fractions: The Building Blocks
Before diving into the equivalence of 1/4 and 3/12, let's solidify our understanding of what a fraction represents. A fraction, at its core, signifies a part of a whole. It's expressed as a ratio of two integers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of equal parts the whole is divided into.
For example, in the fraction 1/4, the numerator (1) represents one part, and the denominator (4) indicates that the whole is divided into four equal parts. This means we are considering one out of four equal parts.
Visualizing Fractions: A Powerful Tool
Visual aids are invaluable when working with fractions, especially for beginners. Imagine a pizza cut into four equal slices. The fraction 1/4 represents one of those four slices. Now, imagine another pizza, but this time, it's cut into twelve equal slices. The fraction 3/12 represents three of those twelve slices.
By visualizing these scenarios, we can begin to intuitively grasp the concept of equivalent fractions—fractions that represent the same portion of a whole, even if they look different.
Exploring Fraction Equivalence: The Core Concept
Two fractions are equivalent if they represent the same value. This means that they represent the same proportion of a whole. The key to determining equivalence lies in the concept of simplifying fractions to their lowest terms. This process involves dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
Let's consider the fraction 3/12. The GCD of 3 and 12 is 3. Dividing both the numerator and the denominator by 3, we get:
3 ÷ 3 / 12 ÷ 3 = 1/4
This demonstrates that 3/12 simplifies to 1/4. Therefore, yes, 1/4 is equivalent to 3/12.
The Multiplicative Property of Equality: Another Approach
Another way to understand fraction equivalence is through the multiplicative property of equality. This property states that multiplying or dividing both the numerator and the denominator of a fraction by the same non-zero number does not change the value of the fraction.
In our case, if we multiply both the numerator and the denominator of 1/4 by 3, we get:
(1 × 3) / (4 × 3) = 3/12
This confirms that 1/4 and 3/12 are equivalent fractions.
Beyond the Basics: Practical Applications of Fraction Equivalence
The concept of fraction equivalence is not merely an abstract mathematical principle; it has widespread practical applications across various fields:
Cooking and Baking: Precise Measurements
In cooking and baking, precise measurements are crucial for achieving the desired results. Recipes often require fractional amounts of ingredients. Understanding fraction equivalence allows cooks and bakers to easily convert measurements, ensuring accuracy and consistency. For instance, if a recipe calls for 1/4 cup of sugar, and you only have a measuring cup marked in twelfths, you'll know that 3/12 cup is the equivalent amount.
Construction and Engineering: Accurate Calculations
In construction and engineering, precise calculations are paramount for structural integrity and safety. Fraction equivalence plays a vital role in ensuring that measurements are accurate and consistent, preventing potential errors that could have serious consequences.
Data Analysis and Statistics: Representing Proportions
In data analysis and statistics, fractions are frequently used to represent proportions and percentages. Understanding fraction equivalence is essential for accurately interpreting and comparing data sets, drawing meaningful conclusions, and making informed decisions.
Financial Calculations: Managing Budgets and Investments
Financial calculations often involve fractions. For example, understanding interest rates, calculating discounts, or managing budgets requires a thorough understanding of fraction equivalence to ensure accuracy and avoid financial errors.
Common Mistakes and How to Avoid Them
While the concept of fraction equivalence seems straightforward, some common mistakes can lead to inaccurate results. Here are a few to watch out for:
Incorrect Simplification: Dividing by the Wrong Number
A common mistake is incorrectly simplifying fractions by dividing the numerator and the denominator by different numbers, rather than their greatest common divisor. This leads to an incorrect equivalent fraction. Always ensure you are dividing by the greatest common divisor to obtain the simplest form of the fraction.
Ignoring the Multiplicative Property: Incorrect Multiplication or Division
Failing to apply the multiplicative property correctly can also lead to errors. Remember that you must multiply or divide both the numerator and the denominator by the same number. Multiplying or dividing only one of them will change the value of the fraction.
Confusing Equivalence with Equality: Understanding the Nuances
It’s crucial to understand the difference between equivalent fractions and equal fractions. While equivalent fractions represent the same portion of a whole, they may not look identical. Equal fractions are fractions that are numerically identical. For instance, 1/4 and 3/12 are equivalent but not equal.
Conclusion: Mastering Fraction Equivalence for Mathematical Proficiency
In conclusion, understanding fraction equivalence is fundamental to mathematical proficiency. It's not merely a concept to be memorized but a principle to be understood and applied. By mastering this concept, you'll develop a stronger grasp of mathematical reasoning, paving the way for success in more advanced mathematical topics. From everyday tasks to complex calculations, the ability to recognize and utilize equivalent fractions is a valuable skill that extends far beyond the classroom. Therefore, take the time to fully grasp this important mathematical concept, and you'll reap the rewards in various aspects of your life. The answer to the initial question, "Is 1/4 equivalent to 3/12?" is a resounding yes, and now you understand the reasons why.
Latest Posts
Latest Posts
-
Why Do Electric Field Lines Never Cross
May 13, 2025
-
1 10 As A Percent And Decimal
May 13, 2025
-
Can All Minerals Be A Gemstone
May 13, 2025
-
Multicellular Heterotrophs Without A Cell Wall
May 13, 2025
-
What Are The Gcf Of 48
May 13, 2025
Related Post
Thank you for visiting our website which covers about Is 1 4 Equivalent To 3 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.