Is 1 2 An Irrational Number
listenit
Apr 02, 2025 · 5 min read
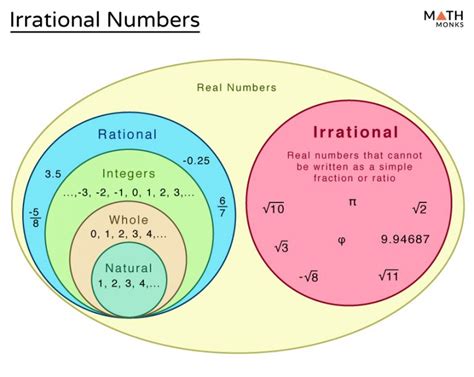
Table of Contents
Is 1/2 an Irrational Number? A Deep Dive into Rational and Irrational Numbers
The question of whether 1/2 is an irrational number is a fundamental one in mathematics, touching upon the core concepts of rational and irrational numbers. The short answer is a resounding no. 1/2 is definitively a rational number. Understanding why requires a closer look at the definitions of these number types and exploring the properties that distinguish them. This article will delve into the specifics, clarifying the distinction and exploring related mathematical concepts.
Understanding Rational Numbers
A rational number is any number that can be expressed as a fraction p/q, where 'p' and 'q' are integers, and 'q' is not zero. The key here is the ability to represent the number as a ratio of two whole numbers. This encompasses a wide range of numbers, including:
- Integers: Whole numbers (both positive and negative), such as -3, 0, 5, etc., can be expressed as fractions (e.g., -3/1, 0/1, 5/1).
- Terminating Decimals: Decimals that end after a finite number of digits, like 0.75 (which is 3/4), 2.5 (which is 5/2), or even 0.3333333 (which is 1/3). While it might seem counterintuitive for repeating decimals, they are still rational due to their fractional representation.
- Repeating Decimals: Decimals with a repeating pattern of digits, such as 0.333... (1/3), 0.142857142857... (1/7), fall under the umbrella of rational numbers. The repeating pattern indicates a fractional representation is possible.
The crucial element is the ability to represent the number precisely as a ratio of two integers. This is where irrational numbers differ significantly.
Defining Irrational Numbers
Irrational numbers are numbers that cannot be expressed as a simple fraction p/q, where 'p' and 'q' are integers, and 'q' is not zero. These numbers have decimal representations that are both non-terminating (they never end) and non-repeating (they don't have a repeating pattern). Famous examples of irrational numbers include:
- π (Pi): The ratio of a circle's circumference to its diameter, approximately 3.14159..., but its decimal representation continues infinitely without any repeating pattern.
- e (Euler's number): The base of the natural logarithm, approximately 2.71828..., also with an infinite, non-repeating decimal expansion.
- √2 (the square root of 2): This number, approximately 1.414..., cannot be expressed as a fraction of two integers. Its decimal representation is infinite and non-repeating. The proof of its irrationality is a classic example in mathematics.
The Proof of 1/2's Rationality
The number 1/2 perfectly fits the definition of a rational number. It's already expressed as a fraction where:
- p = 1 (an integer)
- q = 2 (an integer, and q ≠ 0)
Therefore, 1/2 satisfies all the conditions required for a number to be classified as rational. There is no need for further proof; the representation itself demonstrates its rationality. This contrasts sharply with irrational numbers, which require more intricate proofs to establish their irrationality.
Why the Confusion Might Arise
The potential for confusion might stem from a misunderstanding of decimal representations. While 1/2 has a simple decimal equivalent of 0.5 (a terminating decimal), some might mistakenly assume that only numbers with infinite, non-repeating decimals are irrational. This is incorrect. The defining characteristic is the ability to express the number as a fraction of two integers, regardless of its decimal representation's appearance.
Exploring Further: Types of Rational Numbers
Let's delve deeper into the different types of rational numbers to further solidify the understanding of where 1/2 fits within the broader mathematical context.
Integers
As previously mentioned, integers are a subset of rational numbers. They are whole numbers, including negative numbers and zero. 1/2 is not an integer, as integers do not include fractions or decimals.
Fractions
Fractions are the most direct representation of rational numbers. 1/2 is a fraction in its simplest form; the numerator and denominator share no common factors other than 1. Other equivalent fractions exist (2/4, 3/6, etc.), but they all represent the same rational number.
Decimals
Rational numbers can also be represented as decimals. Terminating decimals, such as 0.5 (which is 1/2), end after a finite number of digits. Repeating decimals, like 0.333... (1/3) also represent rational numbers, despite their infinite decimal representation. The key is the repeating pattern allows for the expression as a fraction.
The Importance of Understanding Rational and Irrational Numbers
The distinction between rational and irrational numbers is fundamental to many areas of mathematics and its applications:
- Algebra: Solving equations and inequalities often involves dealing with both rational and irrational solutions.
- Calculus: Understanding limits and continuity requires a solid grasp of the properties of rational and irrational numbers.
- Geometry: Calculations involving circles, triangles, and other geometric shapes often use irrational numbers like π.
- Number Theory: A branch of mathematics dedicated to exploring the properties of numbers, heavily relies on the distinction between rational and irrational numbers.
Conclusion: 1/2 is Resolutely Rational
In conclusion, the statement "1/2 is an irrational number" is incorrect. 1/2 is a rational number because it can be expressed as a fraction (1/2) where both the numerator and denominator are integers, and the denominator is non-zero. The simplicity of its fractional representation and its terminating decimal form (0.5) further underscores its rationality. Understanding this fundamental distinction is crucial for building a solid foundation in mathematics. The characteristics that define rational and irrational numbers are key to numerous mathematical concepts and applications across various fields. Therefore, remember that the ability to express a number as a ratio of two integers is the definitive criterion for its classification as rational, irrespective of its decimal representation.
Latest Posts
Latest Posts
-
How Does Friction Affect An Objects Motion
Apr 03, 2025
-
How Many Gallons In 12 Pints
Apr 03, 2025
-
Whats The Derivative Of A Constant
Apr 03, 2025
-
The Unit Of Energy In S I Units Is
Apr 03, 2025
-
How Many Fluid Ounces In A Fifth
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Is 1 2 An Irrational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
