Integral Of 1 X 2 A 2
listenit
Jun 14, 2025 · 4 min read
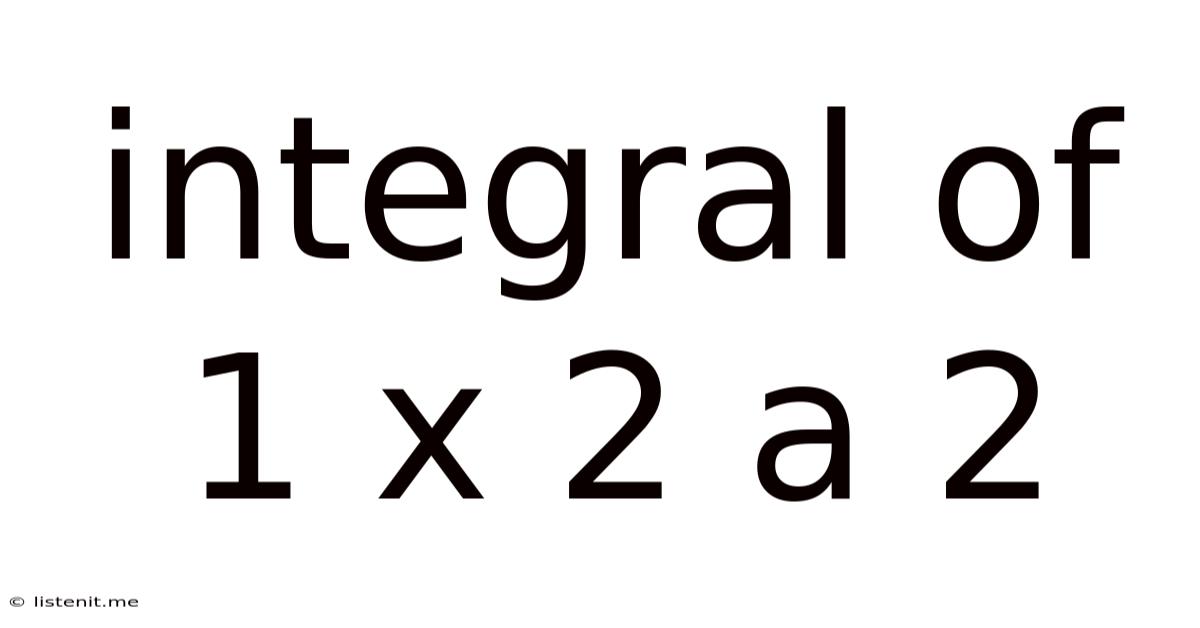
Table of Contents
Exploring the Integral of 1/(x² + a²)
The integral ∫ 1/(x² + a²) dx is a fundamental integral in calculus with widespread applications in various fields, including physics, engineering, and statistics. This comprehensive guide delves into the intricacies of solving this integral, exploring different approaches, and highlighting its significance in practical contexts. We'll examine the solution, its derivation, and common mistakes to avoid. Furthermore, we'll discuss how this integral relates to other important integrals and functions.
Understanding the Problem: ∫ 1/(x² + a²) dx
Our objective is to find the antiderivative of the function f(x) = 1/(x² + a²), where 'a' is a constant. This integral doesn't immediately resemble a standard integration rule, requiring a specific technique for its evaluation. The core challenge lies in recognizing the appropriate substitution or trigonometric identity to simplify the integrand.
Method 1: Trigonometric Substitution
This is the most common and arguably the most elegant method for solving this integral. It leverages the trigonometric identity:
tan²(θ) + 1 = sec²(θ)
-
Substitution: We let x = a tan(θ). This implies dx = a sec²(θ) dθ.
-
Substitution into the Integral: Replacing x and dx in the original integral, we get:
∫ 1/((a tan(θ))² + a²) * a sec²(θ) dθ
- Simplification: The denominator simplifies significantly:
(a tan(θ))² + a² = a²(tan²(θ) + 1) = a²sec²(θ)
The integral now becomes:
∫ 1/(a²sec²(θ)) * a sec²(θ) dθ = ∫ (1/a) dθ
- Integration: This simplified integral is straightforward:
∫ (1/a) dθ = (1/a)θ + C, where C is the constant of integration.
- Back-Substitution: We need to express θ in terms of x. Since x = a tan(θ), we have θ = arctan(x/a).
Therefore, the final solution is:
∫ 1/(x² + a²) dx = (1/a) arctan(x/a) + C
Method 2: Using Partial Fraction Decomposition (Not Applicable Here)
Partial fraction decomposition is a powerful technique for integrating rational functions (fractions of polynomials). However, it's not directly applicable to this particular integral because the denominator, x² + a², is an irreducible quadratic. Partial fraction decomposition works best when the denominator can be factored into linear terms.
Common Mistakes to Avoid
Several common errors can arise when solving this integral:
-
Incorrect Substitution: Using an inappropriate substitution can lead to complex expressions that are difficult to integrate. The substitution x = a tan(θ) is crucial for simplifying the expression. Using other trigonometric substitutions (like x = a sin(θ) or x = a cos(θ)) will not lead to a straightforward solution.
-
Forgetting the Constant of Integration (C): Always remember to include the constant of integration, C, in the final answer. This constant accounts for the family of antiderivatives that share the same derivative.
-
Incorrect Back-Substitution: Carefully track the substitution made and correctly replace θ with its equivalent expression in terms of x after integration.
-
Arithmetic Errors: Double-check your algebraic manipulations and simplification steps to avoid errors.
Applications of the Integral
This seemingly simple integral has surprisingly wide-ranging applications:
-
Physics: It appears frequently in problems involving forces, electric fields, and potential energy calculations. For example, calculating the gravitational potential due to a thin rod requires evaluating a similar integral.
-
Engineering: This integral is fundamental in various engineering disciplines, including electrical engineering (circuit analysis), mechanical engineering (vibration analysis), and civil engineering (structural analysis).
-
Probability and Statistics: The integral is closely related to the probability density function of the Cauchy distribution, a continuous probability distribution that lacks a well-defined mean.
-
Complex Analysis: The integral is also connected to complex analysis through the concept of Cauchy principal value.
Relation to Other Integrals and Functions
The integral of 1/(x² + a²) is closely related to several other important integrals and functions:
-
Inverse Tangent Function: The solution directly involves the inverse tangent (arctan) function, emphasizing the integral's connection to trigonometric functions.
-
Cauchy Distribution: As mentioned, the integral plays a key role in the definition and analysis of the Cauchy distribution.
-
Complex Logarithm: In complex analysis, the integral is closely related to the complex logarithm.
Advanced Considerations: Definite Integrals
When evaluating definite integrals involving 1/(x² + a²), the limits of integration are substituted into the antiderivative obtained previously:
∫<sub>b</sub><sup>a</sup> 1/(x² + a²) dx = (1/a) [arctan(x/a)]<sub>b</sub><sup>a</sup> = (1/a) (arctan(a/a) - arctan(b/a))
Here, 'a' and 'b' represent the upper and lower limits of integration, respectively. Careful calculation of the arctangent values is essential. Remember that the arctangent function has a range of (-π/2, π/2).
Conclusion
The integral ∫ 1/(x² + a²) dx, while seemingly simple, holds significant importance in various mathematical and scientific fields. Mastering its solution through trigonometric substitution is crucial for advanced calculus and its applications. Understanding the nuances of this integral, including its applications and potential pitfalls, equips students and practitioners with a vital tool for problem-solving in diverse domains. Remember to always check your work for errors and pay attention to the constants of integration. Proficiency in solving this integral forms a strong foundation for tackling more complex integration problems in the future.
Latest Posts
Latest Posts
-
Should You Shut Off Water While On Vacation
Jun 15, 2025
-
How To Make A Sticker Sticky Again
Jun 15, 2025
-
How Long To Let Caulk Dry Before Showering
Jun 15, 2025
-
How To Wire Two Lights One Switch
Jun 15, 2025
-
Why Is The Night Sky Orange
Jun 15, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 X 2 A 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.