Integral Of 1 Tanx 1 Tanx
listenit
May 10, 2025 · 5 min read
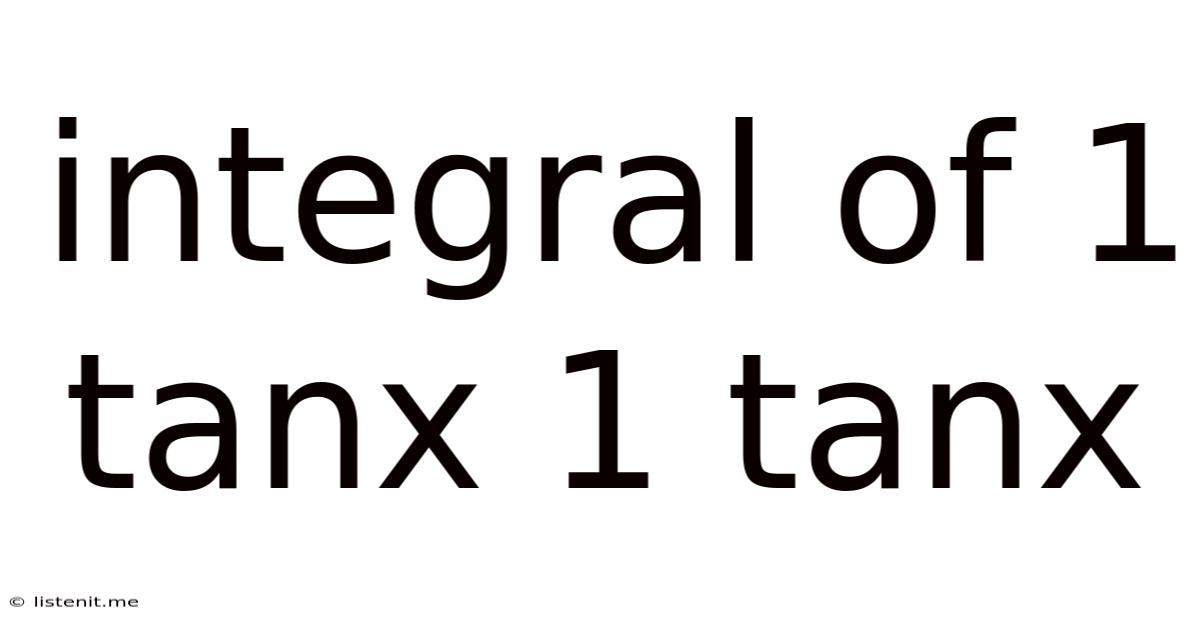
Table of Contents
The Indefinite Integral of 1/(tan x + 1): A Comprehensive Guide
The seemingly simple integral ∫ 1/(tan x + 1) dx can be surprisingly challenging for many students. This comprehensive guide will walk you through various methods to solve this integral, offering a deep dive into the underlying trigonometric identities and techniques involved. We'll explore different approaches, highlighting their advantages and disadvantages, ensuring you gain a thorough understanding of the process.
Understanding the Problem: ∫ 1/(tan x + 1) dx
Before we delve into the solution, let's understand what we're dealing with. The integral involves the tangent function, a trigonometric function defined as the ratio of sine to cosine (tan x = sin x / cos x). The presence of the +1 in the denominator adds another layer of complexity, preventing a straightforward integration. Our goal is to find a function whose derivative is 1/(tan x + 1).
Method 1: Rewriting in Terms of Sine and Cosine
The most common approach is to rewrite the tangent function in terms of its sine and cosine components. This allows for manipulation and simplification that often leads to a solvable integral.
Step 1: Rewrite tan x
We begin by replacing tan x with sin x / cos x:
∫ 1/(sin x / cos x + 1) dx = ∫ 1/((sin x + cos x) / cos x) dx
Step 2: Simplify the Fraction
Simplifying the complex fraction, we get:
∫ cos x / (sin x + cos x) dx
Step 3: A Clever Substitution (Often the Tricky Part)
This is where things get interesting. A simple u-substitution won't work directly. We need a more sophisticated approach. Let's try the following substitution:
Let u = sin x + cos x. Then, du = (cos x - sin x) dx.
Notice that we don't have (cos x - sin x) dx in our integral, but we have cos x dx. This suggests we may need a further manipulation or a different approach.
Step 4: An Alternative Approach for this specific case
Direct substitution isn't directly fruitful here. Let's instead try to manipulate the expression to something more manageable. We can add and subtract sin x from the numerator:
∫ cos x / (sin x + cos x) dx = ∫ (cos x + sin x - sin x) / (sin x + cos x) dx
This cleverly separates the integral into two parts:
∫ (cos x + sin x) / (sin x + cos x) dx - ∫ sin x / (sin x + cos x) dx
The first integral simplifies to ∫ 1 dx = x + C₁
The second integral remains challenging and requires another technique or approximation method. This approach, while providing a partial solution, highlights the limitations of a purely algebraic manipulation.
Method 2: Using a Trigonometric Identity (and a Bit of Trickery)
Let's explore a different route, leveraging a clever trigonometric manipulation. We can rewrite 1/(tan x + 1) by dividing both the numerator and the denominator by cos x:
∫ 1/(tan x + 1) dx = ∫ (1/cos x) / (tan x / cos x + 1/cos x) dx = ∫ sec x / (sec x + tan x) dx
This form doesn't immediately lead to an obvious solution, but it hints at the possibility of a more intricate substitution or the use of a more advanced integration technique.
Method 3: Numerical Methods (When Analytical Solutions Fail)
When analytical methods prove insufficient, numerical methods offer a valuable alternative. These methods approximate the definite integral within a specified range. Popular techniques include:
- Trapezoidal Rule: Approximates the area under the curve using trapezoids.
- Simpson's Rule: Uses parabolas to approximate the area, offering higher accuracy.
- Gaussian Quadrature: Employs strategically chosen points to achieve high accuracy with fewer calculations.
Numerical integration is particularly useful when dealing with integrals that lack closed-form analytical solutions, or when the function is complex or computationally expensive to evaluate directly. Software packages like MATLAB, Mathematica, or Python libraries (SciPy) offer readily available functions to perform these calculations with ease.
Method 4: Exploring the Definite Integral
While finding the indefinite integral is challenging, focusing on the definite integral over a specific interval might provide a more manageable path. Consider the definite integral:
∫[a,b] 1/(tan x + 1) dx
Numerical integration techniques are particularly suitable here. Moreover, if the limits of integration possess specific properties, clever trigonometric identities might simplify the evaluation. For example, if the interval is symmetric around a point where tan x = -1, simplification may be possible.
Why this Integral is Challenging
The integral’s difficulty stems from the interplay between the tangent function and the constant term in the denominator. Standard substitution techniques frequently fall short, requiring creative algebraic manipulation and careful consideration of trigonometric identities. The absence of a straightforward pattern or easily identifiable antiderivative underlines the integral's non-trivial nature.
Advanced Techniques and Considerations:
For those seeking a deeper understanding, more advanced integration techniques could be explored:
- Integration by Parts: While not immediately obvious, a creative application of integration by parts combined with trigonometric identities might lead to a solution, although it's likely to be complex.
- Contour Integration (Complex Analysis): This advanced technique utilizes complex variables and contour integrals to solve certain types of real-valued integrals. It's a powerful but considerably more advanced approach not typically suited for introductory calculus courses.
- Series Expansions: Representing the function as an infinite series (Taylor or Laurent series) might provide an approximate solution, particularly within a restricted range.
Conclusion: A Journey Through Integration
The integral ∫ 1/(tan x + 1) dx exemplifies the complexities and challenges encountered in integral calculus. While a simple closed-form solution isn't readily apparent using standard techniques, a blend of trigonometric manipulation, strategic substitutions (or perhaps a lack thereof), and numerical methods offer viable paths to both approximate and, under certain conditions, find an exact solution. This journey highlights the need for creativity, persistence, and a deep understanding of both algebraic and trigonometric principles in mastering integration. Remember, many integrals lack elegant analytical solutions, and numerical methods are valuable tools in the mathematician's arsenal.
Latest Posts
Latest Posts
-
Is Sand And Water A Homogeneous Mixture
May 11, 2025
-
What Are Two Radioactive Isotopes Of Oxygen
May 11, 2025
-
Is The Square Root Of 14 A Rational Number
May 11, 2025
-
What Is The Mass Number Of Phosphorus
May 11, 2025
-
Give The Complete Electronic Configuration For Ca2
May 11, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 Tanx 1 Tanx . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.