Integral Of 1 A 2 X 2
listenit
Jun 17, 2025 · 5 min read
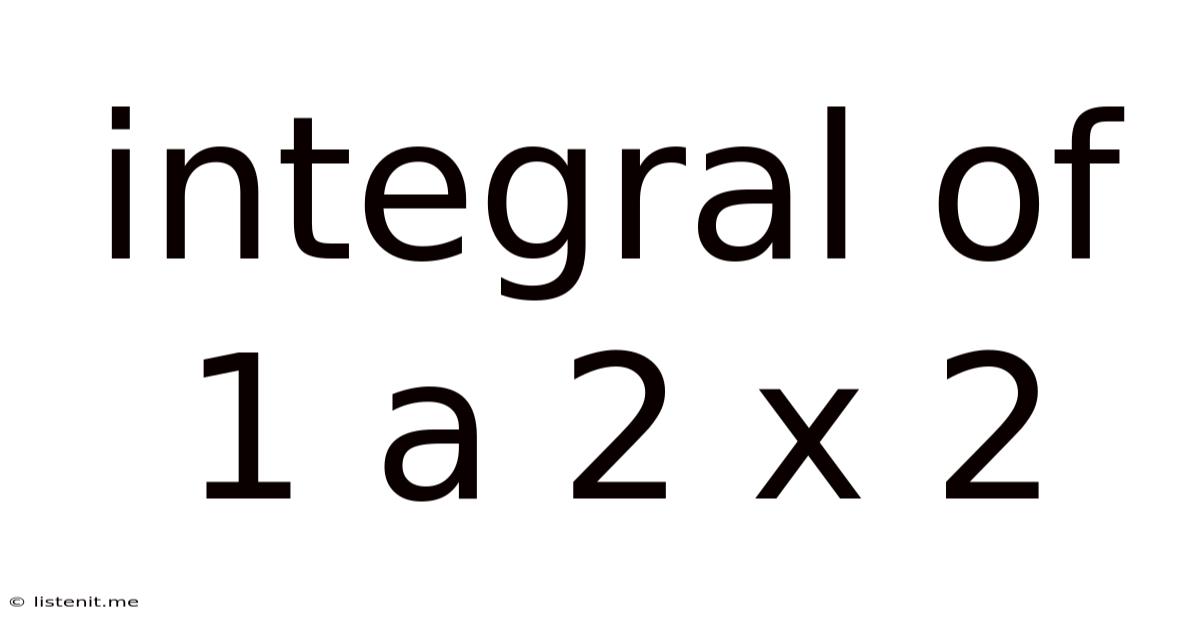
Table of Contents
The Definite Integral of 1/(2x²): A Comprehensive Guide
The seemingly simple definite integral, ∫<sub>a</sub><sup>b</sup> 1/(2x²) dx, presents a fascinating opportunity to explore several key concepts in calculus. While the integrand itself appears straightforward, understanding its nuances and potential pitfalls is crucial for mastering integration techniques. This comprehensive guide delves into the calculation, interpretation, and implications of this integral, catering to both beginners and those seeking a deeper understanding.
Understanding the Integrand: 1/(2x²)
Before we dive into the integration process, let's analyze the integrand, 1/(2x²). This is a rational function, meaning it's a ratio of two polynomials. Specifically, it's a power function with a negative exponent. This negative exponent indicates that the function approaches infinity as x approaches zero. This fact holds significant implications for the boundaries of integration and the existence of the integral itself.
Key Characteristics:
- Power Function: The function is a simple power function of the form kx<sup>n</sup>, where k = 1/2 and n = -2.
- Negative Exponent: The negative exponent signifies an inverse relationship – as x increases, the function value decreases, approaching zero asymptotically. Conversely, as x approaches zero, the function value increases without bound.
- Discontinuity at x = 0: The function is undefined at x = 0, making this point a critical consideration during integration.
The Indefinite Integral: Finding the Antiderivative
To evaluate the definite integral, we first need to determine its indefinite integral, which represents the family of functions whose derivative is 1/(2x²). We can rewrite the integrand as (1/2)x<sup>-2</sup>, making the power rule of integration directly applicable.
The power rule states that the integral of x<sup>n</sup> dx is (x<sup>n+1</sup>)/(n+1) + C, where C is the constant of integration. Applying this rule to our integrand:
∫(1/2)x<sup>-2</sup> dx = (1/2) * (x<sup>-2+1</sup>)/(-2+1) + C = (1/2) * (x<sup>-1</sup>)/(-1) + C = -1/(2x) + C
Therefore, the indefinite integral of 1/(2x²) is -1/(2x) + C, where C represents an arbitrary constant. This constant reflects the fact that multiple functions can share the same derivative (differing only by a constant).
Evaluating the Definite Integral: Applying the Limits of Integration
Now, let's evaluate the definite integral, ∫<sub>a</sub><sup>b</sup> 1/(2x²) dx, using the fundamental theorem of calculus. This theorem states that the definite integral of a function f(x) from a to b is equal to F(b) - F(a), where F(x) is the indefinite integral of f(x).
Applying this theorem to our problem:
∫<sub>a</sub><sup>b</sup> 1/(2x²) dx = [-1/(2x)]<sub>a</sub><sup>b</sup> = (-1/(2b)) - (-1/(2a)) = (1/(2a) - 1/(2b))
This result highlights the crucial role of the limits of integration, 'a' and 'b'. The expression is valid only if both 'a' and 'b' are non-zero and have the same sign (both positive or both negative). This is because the integrand is undefined at x=0 and the integral becomes improper if zero lies within the interval [a,b].
Case 1: Both 'a' and 'b' are positive
If both 'a' and 'b' are positive, the integral represents the area under the curve 1/(2x²) from x = a to x = b. Since the function is always positive in this region, the integral will yield a positive value.
Case 2: Both 'a' and 'b' are negative
Similarly, if both 'a' and 'b' are negative, the integral will also yield a positive value because the function 1/(2x²) is always positive for negative x. However, the geometric interpretation here is less straightforward, representing a signed area below the x-axis.
Case 3: 'a' and 'b' have different signs or zero is included
If 'a' and 'b' have different signs, or if either a or b is zero, the integral becomes improper and requires careful analysis using limits. This case involves considering the limit as one or both bounds approach zero, and might even result in a divergent integral (meaning the integral does not have a finite value).
Improper Integrals and Convergence
The presence of a discontinuity at x = 0 makes the integral improper when the interval [a, b] includes zero. In such cases, we need to approach the evaluation carefully using limits.
For instance, let's consider the integral ∫<sub>-1</sub><sup>1</sup> 1/(2x²) dx. This integral is improper because the integrand has a singularity at x = 0. To evaluate this, we break the integral into two parts:
∫<sub>-1</sub><sup>0</sup> 1/(2x²) dx + ∫<sub>0</sub><sup>1</sup> 1/(2x²) dx
Each of these integrals is evaluated as a limit:
lim<sub>ε→0<sup>+</sup></sub> ∫<sub>-1</sub><sup>-ε</sup> 1/(2x²) dx + lim<sub>ε→0<sup>+</sup></sub> ∫<sub>ε</sub><sup>1</sup> 1/(2x²) dx
Evaluating each limit individually reveals that both integrals diverge (approach infinity). Therefore, the integral ∫<sub>-1</sub><sup>1</sup> 1/(2x²) dx diverges.
Applications and Real-World Examples
While seemingly abstract, integrals like ∫<sub>a</sub><sup>b</sup> 1/(2x²) dx find applications in various fields:
- Physics: This type of integral might appear in calculations related to inverse-square laws, such as gravitational or electrostatic fields. The singularity at x = 0 might correspond to a point mass or charge.
- Probability and Statistics: Similar integrals can arise in probability density functions with inverse-square relationships. Careful handling of the improper integrals becomes crucial for ensuring the normalization of such functions.
- Engineering: In certain engineering problems involving force fields or potential functions, integrals with similar forms may appear, necessitating careful consideration of the limits of integration.
Conclusion: Mastering the Nuances of Integration
The seemingly simple definite integral ∫<sub>a</sub><sup>b</sup> 1/(2x²) dx provides a rich learning experience in integral calculus. It underscores the importance of understanding the properties of the integrand, handling improper integrals correctly, and interpreting the results within the appropriate context. Paying attention to the limits of integration and the potential for divergence is crucial for obtaining accurate and meaningful results. This integral serves as a valuable example for understanding and appreciating the complexities and subtleties inherent within the field of integral calculus. Remember always to carefully consider the domain of the function and the implications of any singularities when working with definite integrals. A deep understanding of these concepts is essential for success in advanced mathematical applications.
Latest Posts
Latest Posts
-
What Is Role Of Saliva In Digestion Of Food
Jun 17, 2025
-
Can Resin Cements Be Used Under Metal Castings
Jun 17, 2025
-
How Does The Musculoskeletal System Maintain Homeostasis
Jun 17, 2025
-
Difference Between Capillary Blood Glucose And Venous Blood Glucose
Jun 17, 2025
-
What Vitamin Is Good For The Pancreas
Jun 17, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 A 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.