How To Write In Logarithmic Form
listenit
Mar 29, 2025 · 6 min read
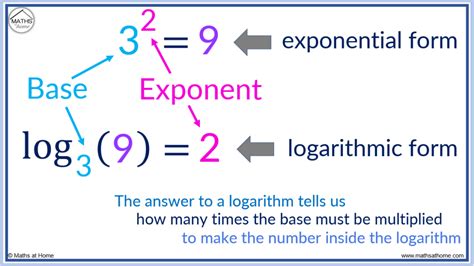
Table of Contents
How to Write in Logarithmic Form: A Comprehensive Guide
Logarithms, while appearing intimidating at first glance, are a fundamental concept in mathematics and science with widespread applications. Understanding how to write expressions in logarithmic form is crucial for mastering various mathematical operations and solving complex problems across diverse fields. This comprehensive guide will demystify the process, providing you with a thorough understanding of logarithms and equipping you with the skills to confidently manipulate logarithmic expressions.
Understanding the Basics of Logarithms
Before diving into the mechanics of writing in logarithmic form, let's establish a solid foundation. A logarithm answers the question: "To what power must we raise a base to obtain a specific number?" This is expressed mathematically as:
log<sub>b</sub>(x) = y
Where:
- b is the base of the logarithm (must be positive and not equal to 1).
- x is the argument (must be positive).
- y is the exponent or logarithm.
This equation is equivalent to the exponential equation:
b<sup>y</sup> = x
This fundamental relationship is the key to converting between logarithmic and exponential forms.
Common Logarithms and Natural Logarithms
Two specific types of logarithms deserve special attention:
-
Common Logarithms: These have a base of 10 and are often written as log(x) without explicitly stating the base. For example, log(100) = 2 because 10² = 100.
-
Natural Logarithms: These have a base of e (Euler's number, approximately 2.718), and are denoted as ln(x). For example, ln(e³) = 3 because e³ = e³.
Understanding the difference between common and natural logarithms is critical, as they are frequently used in various scientific and mathematical applications.
Converting from Exponential Form to Logarithmic Form
This is the most common task when working with logarithms. The process is straightforward: identify the base, exponent, and result in the exponential equation, and then rearrange them into the logarithmic form.
Let's illustrate with some examples:
Example 1:
Exponential form: 2³ = 8
Logarithmic form: log₂(8) = 3 (Here, the base is 2, the exponent is 3, and the result is 8)
Example 2:
Exponential form: 10⁻² = 0.01
Logarithmic form: log(0.01) = -2 (Remember, if the base is not explicitly written, it's assumed to be 10)
Example 3:
Exponential form: e⁴ = x
Logarithmic form: ln(x) = 4 (Here we use the natural logarithm because the base is e)
Example 4: More complex exponential equation
Exponential form: 5^(x+2) = 25
To convert this, we need to simplify first:
5^(x+2) = 5²
Now we can convert:
Logarithmic form: x+2 = log₅(25)
Converting from Logarithmic Form to Exponential Form
The reverse process is equally important. Given a logarithmic expression, you need to identify the base, logarithm, and argument and then rearrange them into the equivalent exponential form.
Example 1:
Logarithmic form: log₃(27) = 3
Exponential form: 3³ = 27
Example 2:
Logarithmic form: log(0.001) = -3
Exponential form: 10⁻³ = 0.001
Example 3:
Logarithmic form: ln(y) = 5
Exponential form: e⁵ = y
Example 4: Logarithmic equation with a coefficient
Logarithmic form: 2log₂(x) = 4
First, simplify:
log₂(x) = 2
Then convert:
Exponential form: 2² = x
Working with Logarithmic Properties
Mastering logarithmic properties is crucial for effectively manipulating logarithmic expressions. These properties allow you to simplify complex equations and solve problems more efficiently. Here are some key properties:
-
Product Rule: log<sub>b</sub>(xy) = log<sub>b</sub>(x) + log<sub>b</sub>(y) The logarithm of a product is the sum of the logarithms.
-
Quotient Rule: log<sub>b</sub>(x/y) = log<sub>b</sub>(x) - log<sub>b</sub>(y) The logarithm of a quotient is the difference of the logarithms.
-
Power Rule: log<sub>b</sub>(xⁿ) = n log<sub>b</sub>(x) The logarithm of a number raised to a power is the product of the power and the logarithm of the number.
-
Change of Base Formula: log<sub>b</sub>(x) = log<sub>a</sub>(x) / log<sub>a</sub>(b) This allows you to change the base of a logarithm to any other base. This is particularly useful when working with calculators that typically only have common or natural logarithm functions.
Applying Logarithmic Properties in Practice
Let's illustrate how to apply these properties to simplify expressions:
Example: Simplify log₂(8x²)
Using the product and power rules:
log₂(8x²) = log₂(8) + log₂(x²) = log₂(2³) + 2log₂(x) = 3 + 2log₂(x)
Solving Logarithmic Equations
Solving logarithmic equations often involves manipulating the equation using logarithmic properties to isolate the variable. Here's a step-by-step approach:
-
Simplify: Use logarithmic properties to combine or separate logarithmic terms.
-
Convert to Exponential Form: If possible, convert the equation to exponential form to solve for the variable.
-
Isolate the Variable: Use algebraic techniques to isolate the variable.
-
Check Your Solution: It's crucial to check your solution in the original equation to ensure it's valid. Remember, the argument of a logarithm must always be positive.
Examples of Solving Logarithmic Equations
Example 1: Solve log₂(x) + log₂(x-2) = 3
-
Simplify: Using the product rule, we get log₂(x(x-2)) = 3
-
Convert to Exponential Form: This becomes 2³ = x(x-2)
-
Isolate the Variable: 8 = x² - 2x, which simplifies to x² - 2x - 8 = 0. Factoring this quadratic equation gives (x-4)(x+2) = 0, resulting in x = 4 or x = -2.
-
Check Your Solution: Since the argument of a logarithm must be positive, x = -2 is an extraneous solution. Therefore, the only valid solution is x = 4.
Example 2: Solve log(x) = 2
This directly converts to exponential form: 10² = x, so x = 100.
Applications of Logarithms
Logarithms have far-reaching applications in various fields:
-
Chemistry: pH calculations (measuring acidity or alkalinity).
-
Physics: Measuring sound intensity (decibels), earthquake magnitude (Richter scale).
-
Finance: Calculating compound interest, modelling exponential growth.
-
Computer Science: Computational complexity analysis of algorithms.
-
Signal Processing: Analyzing signals and frequencies.
Understanding how to write in logarithmic form is essential for utilizing these applications effectively. The ability to convert between logarithmic and exponential forms and apply logarithmic properties allows for simplification and solution of complex problems within these fields.
Conclusion
Writing in logarithmic form is a fundamental skill in mathematics and related fields. This guide has equipped you with the knowledge and tools to confidently convert between exponential and logarithmic forms, apply logarithmic properties, and solve logarithmic equations. Remember, practice is key to mastering these concepts. By regularly working through examples and applying these principles to different problems, you will build a strong understanding of logarithms and unlock their vast potential in problem-solving across various disciplines. The more you engage with this mathematical tool, the more comfortable and confident you will become in handling logarithmic expressions with ease.
Latest Posts
Latest Posts
-
Oz In A Fifth Of Alcohol
Apr 01, 2025
-
What Is To The 1 2 Power
Apr 01, 2025
-
Is Water Evaporating A Chemical Or Physical Change
Apr 01, 2025
-
Which Two Elements Make Up Water
Apr 01, 2025
-
How To Find A Unit Vector
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How To Write In Logarithmic Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
