How To Write 20 As A Fraction
listenit
Mar 26, 2025 · 6 min read
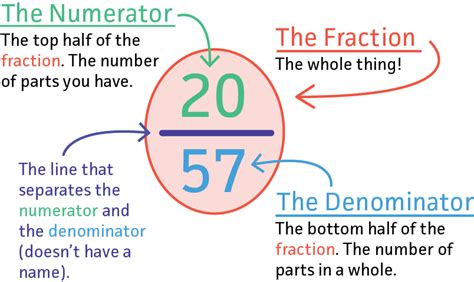
Table of Contents
How to Write 20 as a Fraction: A Comprehensive Guide
Writing a whole number, like 20, as a fraction might seem trivial at first glance. However, understanding the underlying principles and exploring the various possibilities opens up a world of mathematical flexibility and problem-solving opportunities. This comprehensive guide delves into the different ways to represent 20 as a fraction, highlighting the significance of equivalent fractions and the implications for various mathematical applications.
Understanding Fractions: A Quick Refresher
Before diving into the specific representations of 20 as a fraction, let's briefly review the fundamental concept of a fraction. A fraction represents a part of a whole. It is expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts considered, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator (representing 3 parts) and 4 is the denominator (representing a whole divided into 4 equal parts).
The Simplest Form: 20/1
The most straightforward way to write 20 as a fraction is to express it as 20/1. This signifies that we have 20 parts out of a total of 1 whole. While seemingly simple, this representation is crucial because it establishes the foundation for understanding how whole numbers can be expressed fractionally. It emphasizes that every whole number can be considered as a fraction with a denominator of 1. This form is particularly useful when performing operations involving fractions and whole numbers. For instance, when adding a fraction to a whole number, converting the whole number to a fraction with a denominator of 1 allows for a common denominator to be established, facilitating the addition process.
Equivalent Fractions: Exploring the Possibilities
A key concept in working with fractions is the idea of equivalent fractions. Equivalent fractions represent the same value but are expressed with different numerators and denominators. We can generate countless equivalent fractions for 20 by multiplying both the numerator and the denominator by the same non-zero number. This principle ensures that the ratio remains unchanged, maintaining the same value.
Let's explore some examples:
- Multiplying by 2: 20/1 * 2/2 = 40/2. This means 20 is equivalent to 40/2.
- Multiplying by 3: 20/1 * 3/3 = 60/3. Therefore, 20 is also equivalent to 60/3.
- Multiplying by 4: 20/1 * 4/4 = 80/4. Similarly, 20 equals 80/4.
This process can be repeated indefinitely, generating an infinite number of equivalent fractions for 20. The choice of which equivalent fraction to use depends entirely on the context of the problem. Sometimes, a specific denominator is required for calculations or comparisons, while other times, a simplified fraction might be preferred for clarity.
Simplifying Fractions: Finding the Lowest Terms
While we can create an infinite number of equivalent fractions, it's often beneficial to express a fraction in its simplest form, also known as its lowest terms. A fraction is in its simplest form when the greatest common divisor (GCD) of the numerator and denominator is 1. In simpler terms, this means there's no number other than 1 that divides both the numerator and denominator without leaving a remainder.
Since 20/1 is already in its simplest form (the GCD of 20 and 1 is 1), other equivalent fractions, such as 40/2, 60/3, etc., are not in their simplest form. They can be simplified by dividing both the numerator and the denominator by their GCD. For instance, the GCD of 40 and 2 is 2, so 40/2 simplifies to 20/1. Similarly, the GCD of 60 and 3 is 3, simplifying 60/3 to 20/1.
This simplification process is crucial for simplifying calculations and making fractions easier to understand and interpret. Using the simplest form enhances clarity and avoids unnecessary complexity in mathematical expressions.
Practical Applications: Why This Matters
The ability to represent 20, or any whole number, as a fraction is far from a mere mathematical curiosity. It has significant practical applications across various fields:
1. Working with Ratios and Proportions:
Many real-world problems involve ratios and proportions. Expressing whole numbers as fractions allows for consistent calculations and comparisons. For example, if a recipe calls for a ratio of 20 parts flour to 5 parts sugar, we can express this as 20/5, which simplifies to 4/1, indicating a 4:1 ratio.
2. Solving Equations and Inequalities:
In algebra, fractions are frequently encountered. Being able to represent whole numbers as fractions allows for smooth integration within equations and inequalities involving fractions. This ensures that solutions can be expressed consistently, regardless of the presence of whole numbers or fractions.
3. Calculating Percentages:
Percentages are essentially fractions with a denominator of 100. Representing whole numbers as fractions allows for easier conversion to percentages. For example, to express 20 as a percentage, we can write it as 20/1, then multiply the numerator and denominator by 100 to obtain 2000/100, which is equivalent to 2000%.
4. Geometry and Measurement:
In geometry, fractions often arise when dealing with measurements and areas. For example, if a rectangle has a length of 20 units and a width of 1 unit, the area can be expressed as 20/1 square units.
5. Data Analysis and Statistics:
In data analysis, fractions and ratios are used extensively to represent proportions and probabilities. The ability to work with whole numbers as fractions ensures consistent data representation and analysis.
Beyond the Basics: Exploring More Complex Scenarios
While expressing 20 as 20/1 and its equivalent fractions is fundamental, let's consider scenarios that require a more nuanced approach:
-
Fractions with specific denominators: Suppose a problem requires a fraction with a denominator of 10. To represent 20 with a denominator of 10, we can set up a proportion: 20/1 = x/10. Solving for x, we get x = 200. Therefore, 20 can be represented as 200/10. This demonstrates how we can find an equivalent fraction with a specified denominator.
-
Improper Fractions: While 20/1 is a proper fraction (the numerator is less than the denominator), we can also represent 20 as an improper fraction by selecting a denominator other than 1 and appropriately adjusting the numerator. For example, 40/2, 60/3 are improper fractions that are equivalent to 20. Improper fractions are valuable in various calculations, especially when dealing with mixed numbers.
Conclusion: Mastering the Art of Fraction Representation
The seemingly simple act of writing 20 as a fraction reveals a wealth of mathematical concepts and practical applications. Understanding equivalent fractions, simplifying to lowest terms, and recognizing the flexibility in representing whole numbers fractionally empowers one to solve a diverse range of problems across various disciplines. The seemingly trivial act of writing 20 as a fraction becomes a cornerstone of mathematical fluency, enabling effective problem-solving and a deeper understanding of numerical relationships. By mastering these foundational concepts, you equip yourself with essential tools for navigating complex mathematical challenges and confidently tackling real-world applications.
Latest Posts
Latest Posts
-
Least Common Multiple Of 10 And 8
Mar 29, 2025
-
Name 3 Ways To Dissolve Something Faster
Mar 29, 2025
-
Charged Language In I Have A Dream
Mar 29, 2025
-
What Percentage Is 38 Out Of 40
Mar 29, 2025
-
What Does The Prefix Hydro Mean
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about How To Write 20 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
