How To Find The Radius Of A Circle Using Circumference
listenit
Mar 26, 2025 · 5 min read
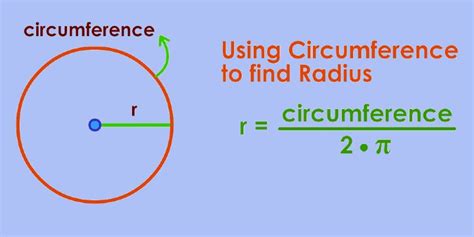
Table of Contents
How to Find the Radius of a Circle Using Circumference
Determining the radius of a circle given its circumference is a fundamental concept in geometry with applications spanning various fields, from engineering and architecture to computer graphics and data analysis. This comprehensive guide will delve into the methods for calculating the radius, exploring different approaches, tackling potential challenges, and offering practical examples to solidify your understanding.
Understanding the Relationship Between Radius and Circumference
Before we embark on the calculation process, let's establish the fundamental relationship between a circle's radius and its circumference. The circumference (C) of a circle is the distance around its edge. It's directly proportional to the radius (r), the distance from the center of the circle to any point on its circumference. This relationship is encapsulated in the well-known formula:
C = 2πr
Where:
- C represents the circumference of the circle.
- r represents the radius of the circle.
- π (pi) is a mathematical constant, approximately equal to 3.14159. It represents the ratio of a circle's circumference to its diameter.
This formula forms the bedrock of our calculations. By rearranging it, we can derive a formula to directly calculate the radius from the circumference.
Deriving the Formula for Radius from Circumference
To find the radius (r) when the circumference (C) is known, we need to rearrange the circumference formula:
C = 2πr
To isolate 'r', we can follow these steps:
-
Divide both sides by 2π: This cancels out the '2π' on the right side, leaving 'r' by itself.
r = C / 2π
This is our crucial formula. It states that the radius of a circle is equal to its circumference divided by 2π.
Step-by-Step Calculation of Radius from Circumference
Now let's break down the process of calculating the radius using a step-by-step approach, incorporating real-world examples:
Example 1: Finding the Radius of a Circular Garden
Let's say you have a circular garden with a circumference of 30 meters. To find the radius:
-
Write down the given circumference: C = 30 meters
-
Use the formula: r = C / 2π
-
Substitute the value of C: r = 30 meters / 2π
-
Use the approximation for π (3.14159): r ≈ 30 meters / (2 * 3.14159)
-
Calculate: r ≈ 30 meters / 6.28318 ≈ 4.77 meters
Therefore, the radius of your circular garden is approximately 4.77 meters.
Example 2: Calculating Radius of a Circular Track
Imagine a circular running track with a circumference of 400 meters. Let's find its radius:
-
Given circumference: C = 400 meters
-
Formula: r = C / 2π
-
Substitution: r = 400 meters / 2π
-
Calculation using π ≈ 3.14159: r ≈ 400 meters / 6.28318 ≈ 63.66 meters
The radius of the circular running track is approximately 63.66 meters.
Handling Different Units of Measurement
It's crucial to maintain consistency in units throughout your calculations. If the circumference is given in centimeters, the radius will also be in centimeters. Similarly, if the circumference is in feet, inches, kilometers, or any other unit, the resulting radius will have the same unit. Inconsistent units will lead to incorrect results.
Dealing with Complex Scenarios and Potential Challenges
While the basic calculation is straightforward, some scenarios may present minor challenges:
-
Circumference with Uncommon Units: If the circumference is given in less common units, you might need to convert them to standard units (like meters or centimeters) before applying the formula. For example, if the circumference is given in yards, convert it to meters using the appropriate conversion factor (1 yard ≈ 0.9144 meters).
-
Dealing with Approximations: Remember that π is an irrational number, meaning its decimal representation goes on infinitely. Using an approximation of π (like 3.14 or 3.14159) will introduce a small degree of error into your final answer. For most practical purposes, using 3.14159 provides sufficient accuracy. However, for extremely precise calculations, you might need to use a more precise value of π provided by your calculator or software.
-
Using Scientific Calculators and Software: Most scientific calculators and mathematical software packages have built-in functions for π, making the calculations faster and more accurate. Leveraging these tools can streamline the process, especially when dealing with multiple calculations or complex scenarios.
-
Real-World Measurement Inaccuracies: When working with real-world measurements, remember that there's always a certain degree of inherent measurement error. This uncertainty should be considered when interpreting the calculated radius.
Advanced Applications and Related Concepts
The ability to calculate the radius from the circumference is a foundational concept that extends to more complex geometrical problems:
-
Area Calculation: Once you've found the radius, you can easily calculate the area of the circle using the formula: Area = πr².
-
Sector and Segment Calculations: Understanding radius allows you to calculate the area of sectors (portions of a circle defined by two radii and an arc) and segments (regions bounded by a chord and an arc).
-
Three-Dimensional Applications: The concept extends to calculating the volume and surface area of three-dimensional shapes like cylinders, cones, and spheres, which all involve circular components.
-
Applications in Engineering and Design: In fields like engineering and design, determining the radius from the circumference is critical for various tasks, including designing pipelines, calculating the stress on circular structures, and more.
Conclusion: Mastering Radius Calculation from Circumference
Calculating the radius of a circle using its circumference is a fundamental skill in geometry with wide-ranging practical applications. By mastering the formula and understanding the associated concepts, you'll be equipped to tackle various geometrical problems and real-world applications effectively. Remember to always maintain consistent units, account for approximations in π, and leverage appropriate tools for accurate and efficient calculations. This knowledge will not only enhance your mathematical understanding but will also prove invaluable in various academic and professional contexts.
Latest Posts
Latest Posts
-
Why Are Most Fossils Found In Sedimentary Rocks
Mar 29, 2025
-
What Is The Gcf Of 45 And 36
Mar 29, 2025
-
What Number Is 45 Of 90
Mar 29, 2025
-
What Is 2 5 As A Decimal
Mar 29, 2025
-
18 As A Percentage Of 60
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about How To Find The Radius Of A Circle Using Circumference . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
