How To Find Perimeter Of Equilateral Triangle
listenit
Apr 07, 2025 · 5 min read
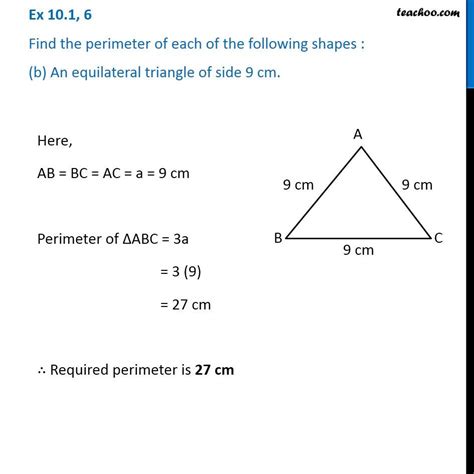
Table of Contents
How to Find the Perimeter of an Equilateral Triangle: A Comprehensive Guide
The perimeter of any polygon, including a triangle, is simply the total distance around its exterior. While calculating the perimeter of irregular triangles requires finding the length of each side individually, the equilateral triangle offers a delightful shortcut thanks to its defining characteristic: all three sides are equal in length. This simplicity makes calculating its perimeter remarkably straightforward. This comprehensive guide will delve into various methods to find the perimeter of an equilateral triangle, catering to different levels of mathematical understanding. We'll explore basic methods, delve into more advanced concepts, and even touch upon real-world applications.
Understanding Equilateral Triangles
Before we jump into the calculations, let's solidify our understanding of what makes an equilateral triangle unique. An equilateral triangle is a polygon with three sides of equal length and three angles of equal measure (60° each). This consistent geometry is the key to simplifying perimeter calculations.
Key Properties of Equilateral Triangles:
- Equal Sides: All three sides possess identical lengths.
- Equal Angles: Each interior angle measures exactly 60 degrees.
- Symmetry: It exhibits perfect rotational and reflectional symmetry.
Method 1: The Basic Formula
The simplest and most direct way to determine the perimeter of an equilateral triangle is to use the fundamental formula:
Perimeter = 3 * side length
Where:
- Perimeter represents the total distance around the triangle.
- Side length refers to the length of any one side (since all sides are equal).
Example:
If an equilateral triangle has a side length of 5 cm, its perimeter is calculated as follows:
Perimeter = 3 * 5 cm = 15 cm
Method 2: Using the Area and Height
While less direct than the basic formula, this method demonstrates the relationship between a triangle's area, height, and perimeter. It involves using the formula for the area of an equilateral triangle and then working backward to find the side length and subsequently the perimeter.
The area of an equilateral triangle can be calculated using the following formula:
Area = (√3/4) * side length²
To find the side length from the area:
Side length = √(4 * Area / √3)
Once the side length is found, simply multiply it by 3 to get the perimeter.
Example:
If the area of an equilateral triangle is 25√3 square cm, the side length can be calculated as follows:
Side length = √(4 * 25√3 / √3) = √100 = 10 cm
Therefore, the perimeter is:
Perimeter = 3 * 10 cm = 30 cm
This method is useful when the area of the triangle is known instead of the side length.
Method 3: Applying Trigonometry
For those with a stronger background in trigonometry, we can utilize trigonometric functions to determine the side length and subsequently the perimeter. If we know the height (altitude) of the equilateral triangle, we can use the trigonometric relationship within a 30-60-90 triangle (formed by drawing an altitude).
In a 30-60-90 triangle, the ratio of sides is 1:√3:2. Knowing the height allows us to find the side length using this ratio.
Side length = (2/√3) * height
Then, as always, multiply the side length by 3 to obtain the perimeter.
Example:
If the height of an equilateral triangle is 10√3 cm, the side length is:
Side length = (2/√3) * 10√3 cm = 20 cm
Perimeter = 3 * 20 cm = 60 cm
Method 4: Circumradius and Inradius
The circumradius (R) is the radius of the circle that circumscribes the equilateral triangle (passes through all three vertices). The inradius (r) is the radius of the circle inscribed within the triangle (touches all three sides). Both can be used to find the side length and, subsequently, the perimeter.
Using Circumradius (R):
Side length = R√3
Perimeter = 3R√3
Using Inradius (r):
Side length = 2r√3
Perimeter = 6r√3
These methods are particularly useful when the circumcenter or incenter and its radius are given or easily determinable.
Method 5: Coordinate Geometry
If the vertices of the equilateral triangle are defined by coordinates on a Cartesian plane, we can use the distance formula to find the length of each side. The distance formula between two points (x₁, y₁) and (x₂, y₂) is:
Distance = √[(x₂ - x₁)² + (y₂ - y₁)²]
Calculate the distance between each pair of vertices. Since it's an equilateral triangle, all three distances will be equal. Multiply this distance by 3 to find the perimeter.
Real-World Applications of Equilateral Triangle Perimeter Calculations
Understanding how to calculate the perimeter of an equilateral triangle isn't just an academic exercise. It has practical applications in various fields:
- Engineering: Calculating the lengths of structural components in bridges, buildings, or other constructions frequently involves working with equilateral triangles.
- Architecture: Designing aesthetically pleasing structures often incorporates equilateral triangles, and determining their perimeter is crucial for material estimation and planning.
- Design: In graphic design, logos, and other visual elements frequently feature equilateral triangles, requiring precise perimeter calculations for accurate scaling and reproduction.
- Construction: Equilateral triangles are used in frameworks and support structures. Knowing their perimeter helps in material estimation and efficient design.
- Cartography: When dealing with geographic coordinates, understanding geometric relationships, including the perimeter of equilateral triangles, can be helpful in mapping and surveying.
Advanced Concepts and Further Exploration
For those interested in delving deeper, exploring concepts such as:
- Similar Triangles: Understanding similar triangles and their proportional relationships can provide alternative methods for perimeter calculation.
- Vector Geometry: Using vectors to represent the sides of the triangle allows for a more abstract and potentially efficient approach to determining the perimeter.
- Calculus: While not directly necessary for basic perimeter calculations, calculus can be applied to explore the relationship between the perimeter and other properties of the equilateral triangle in a more sophisticated manner.
Conclusion
Calculating the perimeter of an equilateral triangle is a fundamental concept in geometry with various practical applications. Whether you use the simple formula, employ trigonometry, or utilize area relationships, the core principle remains the same: leverage the equal side lengths inherent to an equilateral triangle to simplify the calculation. This comprehensive guide provides a versatile toolkit for approaching this problem, empowering you with the knowledge and methods to tackle it confidently, regardless of the information provided. Remember to choose the method most appropriate for the given data and your level of mathematical understanding. Mastering this concept opens doors to solving more complex geometric problems and understanding the world around us better.
Latest Posts
Latest Posts
-
Square Root Of 216 In Simplest Radical Form
Apr 09, 2025
-
Difference Between A Compound And A Solution
Apr 09, 2025
-
How Many Right Angles Does A Rectangle Have
Apr 09, 2025
-
How Does Light Go From Red To Viowelt
Apr 09, 2025
-
What Isotope Has 13 Protons And 14 Neutrons
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about How To Find Perimeter Of Equilateral Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.