How To Find Amplitude Period And Phase Shift
listenit
Apr 02, 2025 · 5 min read
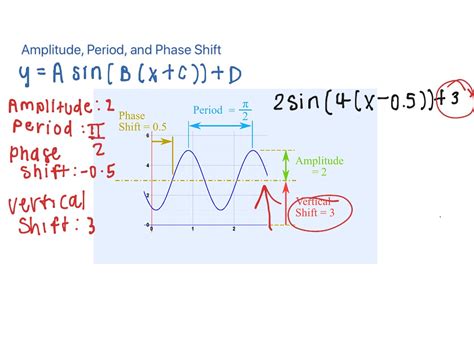
Table of Contents
- How To Find Amplitude Period And Phase Shift
- Table of Contents
- How to Find Amplitude, Period, and Phase Shift: A Comprehensive Guide
- Understanding the Basics: Sine and Cosine Functions
- Finding Amplitude, Period, and Phase Shift: Step-by-Step Guide
- 1. Identifying the Amplitude
- 2. Determining the Period
- 3. Calculating the Phase Shift
- Working with Different Forms of Trigonometric Functions
- a) Functions with a Different Coefficient for x
- b) Functions with Coefficients Outside the Parentheses
- c) Functions with a Vertical Shift (Midline Change)
- d) Functions Involving Secant and Cosecant
- e) Functions Involving Tangent and Cotangent
- Graphical Representation and Verification
- Advanced Applications and Considerations
- Troubleshooting and Common Mistakes
- Latest Posts
- Latest Posts
- Related Post
How to Find Amplitude, Period, and Phase Shift: A Comprehensive Guide
Understanding amplitude, period, and phase shift is crucial for anyone working with periodic functions, especially in fields like physics, engineering, and signal processing. These parameters describe the key characteristics of waves and oscillations, allowing us to analyze and predict their behavior. This comprehensive guide will walk you through the process of finding these values for various trigonometric functions, providing clear explanations and practical examples.
Understanding the Basics: Sine and Cosine Functions
The foundation of understanding amplitude, period, and phase shift lies in grasping the basic sine and cosine functions. Let's review their standard forms:
- Sine function:
y = A sin(Bx - C) - Cosine function:
y = A cos(Bx - C)
Where:
-
A represents the amplitude: This is the vertical distance from the midline of the graph to its peak or trough. It essentially dictates the height of the wave. A larger amplitude means a taller wave.
-
B influences the period: The period (denoted by T) is the horizontal distance it takes for the function to complete one full cycle. It's calculated as
T = 2π/|B|. A larger B value means a shorter period, resulting in a more compressed wave. -
C determines the phase shift: This represents a horizontal shift of the graph. A positive C value shifts the graph to the right, while a negative C value shifts it to the left. The phase shift is calculated as
C/B.
Finding Amplitude, Period, and Phase Shift: Step-by-Step Guide
Let's break down the process of extracting these parameters from different forms of trigonometric functions.
1. Identifying the Amplitude
The amplitude, |A|, is the absolute value of the coefficient multiplying the trigonometric function (sine or cosine). It's always a positive value.
Example:
In the function y = 3sin(2x - π), the amplitude is |3| = 3.
2. Determining the Period
The period is calculated using the formula T = 2π/|B|, where B is the coefficient of x within the trigonometric function.
Example:
In the function y = 3sin(2x - π), B = 2. Therefore, the period is T = 2π/|2| = π.
3. Calculating the Phase Shift
The phase shift is calculated as C/B, where C is the constant term subtracted from Bx within the parenthesis of the trigonometric function. Remember, a positive phase shift indicates a shift to the right, while a negative phase shift indicates a shift to the left.
Example:
In the function y = 3sin(2x - π), B = 2 and C = π. Therefore, the phase shift is π/2. This means the graph is shifted π/2 units to the right.
Working with Different Forms of Trigonometric Functions
Trigonometric functions can be presented in various forms. Let's explore how to extract amplitude, period, and phase shift from some common variations.
a) Functions with a Different Coefficient for x
Consider a function like y = 4cos(3x + π/2). Here, B = 3 and C = -π/2.
- Amplitude: |4| = 4
- Period:
2π/|3| = 2π/3 - Phase Shift:
(-π/2)/3 = -π/6(A shift of π/6 units to the left)
b) Functions with Coefficients Outside the Parentheses
Functions can sometimes have coefficients outside the parentheses, affecting the vertical scaling but not the period or phase shift. For instance: y = 2(sin(x - π/4)). The '2' stretches the graph vertically.
- Amplitude: |2| = 2
- Period:
2π/|1| = 2π(B=1 since it's implicitly multiplied by x) - Phase Shift:
π/4(A shift of π/4 units to the right)
c) Functions with a Vertical Shift (Midline Change)
A vertical shift changes the midline of the graph. This is represented by adding or subtracting a constant to the entire function. For example, y = sin(x) + 2.
- Amplitude: |1| = 1
- Period:
2π/|1| = 2π - Phase Shift: 0
- Vertical Shift: +2 (The midline is shifted up by 2 units).
d) Functions Involving Secant and Cosecant
The secant (sec x) and cosecant (csc x) functions are reciprocals of cosine and sine, respectively. They don't have amplitude in the same way as sine and cosine, but their period and phase shifts can be determined by considering their related cosine and sine functions. The period for both is 2π, and phase shifts are determined by the argument within the function.
Example: y = 2sec(x - π/3)
- Period: 2π
- Phase Shift: π/3 (rightward shift)
e) Functions Involving Tangent and Cotangent
The tangent (tan x) and cotangent (cot x) functions have periods of π instead of 2π. The same principles apply for calculating phase shifts.
Example: y = 3tan(2x + π/2)
- Period:
π/|2| = π/2 - Phase Shift:
(π/2)/2 = π/4(leftward shift)
Graphical Representation and Verification
Plotting the graph of the function helps visualize the amplitude, period, and phase shift. Online graphing calculators or software packages are useful tools for this. By comparing the graph to the standard sine or cosine wave, you can visually confirm the values you calculated.
Advanced Applications and Considerations
The concepts of amplitude, period, and phase shift extend beyond basic trigonometric functions. They are integral to understanding:
- Fourier analysis: This technique decomposes complex waveforms into simpler sinusoidal components, each with its own amplitude, period, and phase.
- Signal processing: Analyzing signals like audio or electrical signals requires understanding their frequency components, which are directly related to period.
- Physics: Describing oscillations and waves, like sound waves or electromagnetic waves, heavily relies on these parameters.
Troubleshooting and Common Mistakes
- Incorrect sign for phase shift: Remember that a positive C value leads to a rightward shift, and a negative C value leads to a leftward shift.
- Forgetting the absolute value for amplitude and period: Amplitude and the period calculation always result in positive values.
- Confusing B and C: Pay close attention to which constant is multiplying x and which one is being subtracted or added.
- Improper handling of functions other than sine and cosine: Remember the different period values for tangent, cotangent, secant, and cosecant.
By carefully following the steps outlined above and practicing with various examples, you can confidently determine the amplitude, period, and phase shift of any trigonometric function. Remember to visualize the results using graphical representations to solidify your understanding. Through consistent practice and careful attention to detail, mastering these concepts will open up a world of possibilities in understanding and analyzing periodic phenomena.
Latest Posts
Latest Posts
-
Does A Trapezoid Have 4 Right Angles
Apr 08, 2025
-
The Central Part Of An Atom Containing Protons And Neutrons
Apr 08, 2025
-
Position The Following Items In Order Of Decreasing Size
Apr 08, 2025
-
Whats The Square Root Of 108
Apr 08, 2025
-
What Are The Two Most Common Elements In Earths Crust
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about How To Find Amplitude Period And Phase Shift . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.