How Much Is 3/4 Times 2
listenit
May 25, 2025 · 4 min read
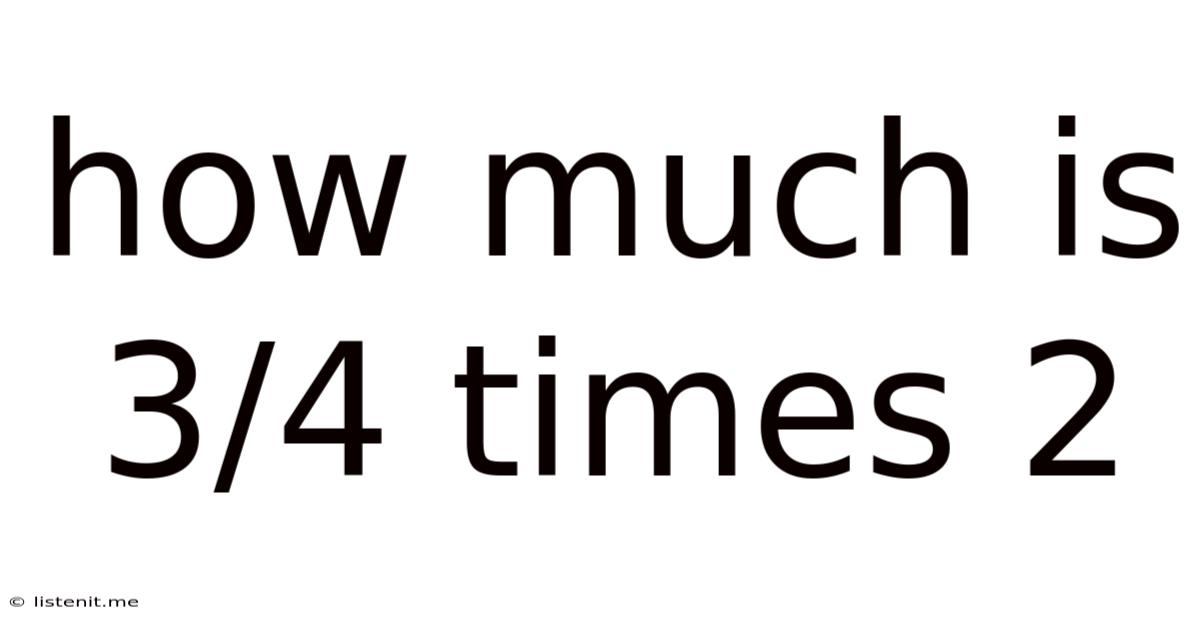
Table of Contents
Decoding the Simple Calculation: How Much is 3/4 Times 2?
This seemingly simple arithmetic problem, "How much is 3/4 times 2?", can serve as a gateway to understanding fundamental concepts in mathematics, particularly fractions and multiplication. While the answer itself is straightforward, exploring the various methods of solving it and its implications opens doors to deeper mathematical understanding. This article will delve into different approaches, provide visual aids, and discuss the relevance of this seemingly simple calculation in real-world applications.
Understanding Fractions and Multiplication
Before tackling the problem, let's refresh our understanding of fractions and multiplication. A fraction represents a part of a whole. The top number (numerator) indicates the number of parts we have, and the bottom number (denominator) indicates the total number of equal parts the whole is divided into. Multiplication, in its simplest form, is repeated addition. When we multiply a fraction by a whole number, we're essentially adding the fraction to itself that many times.
Method 1: Direct Multiplication
The most straightforward approach to solving 3/4 times 2 is direct multiplication:
(3/4) * 2 = (3 * 2) / 4 = 6/4
This method involves multiplying the numerator (3) by the whole number (2) and keeping the denominator (4) the same. The result, 6/4, is an improper fraction (where the numerator is larger than the denominator).
Method 2: Converting to a Mixed Number
An improper fraction like 6/4 can be converted into a mixed number, which combines a whole number and a proper fraction. To do this, we divide the numerator (6) by the denominator (4):
6 ÷ 4 = 1 with a remainder of 2
This means that 6/4 is equal to 1 and 2/4. Further simplification is possible:
2/4 simplifies to 1/2 by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 2.
Therefore, 6/4 = 1 1/2 or 1.5
This representation makes the answer easier to grasp intuitively. We have one whole and one-half.
Method 3: Visual Representation
A visual approach can enhance understanding, especially for those who benefit from concrete examples. Imagine a circle divided into four equal parts. 3/4 represents three of these four parts. Multiplying by 2 means we have two sets of these three-quarters:
[Insert image here: Two circles, each divided into fourths, with three-fourths shaded in each. The total shaded area represents 1 and 1/2 circles.]
This visual representation clearly shows that 3/4 times 2 equals 1 and a half.
Method 4: Converting to Decimals
Another method involves converting the fraction to a decimal before multiplying:
3/4 = 0.75
Then, multiply the decimal by 2:
0.75 * 2 = 1.5
This method is particularly useful when dealing with more complex calculations or when using calculators.
Real-World Applications
The calculation "3/4 times 2" may seem trivial in isolation, but its application extends to various real-world scenarios:
-
Cooking and Baking: Recipes often require fractional measurements. If a recipe calls for 3/4 cup of flour and you need to double the recipe, you'll need to calculate 3/4 times 2.
-
Construction and Measurement: Many construction projects involve fractional measurements of length, width, or volume. Scaling up or down a project often requires multiplying fractions by whole numbers.
-
Finance and Budgeting: Calculating percentages, discounts, or interest rates often involves fractional calculations. For instance, determining the interest on a loan involving 3/4 of a specific amount.
-
Data Analysis: In statistical analysis and data visualization, fractions are used extensively. Scaling data sets or calculating proportions may involve multiplying fractions by whole numbers or other fractions.
Expanding the Concept: Multiplying Fractions by Fractions
While this article focuses on multiplying a fraction by a whole number, understanding the principle extends to multiplying fractions by other fractions. The general rule is:
(a/b) * (c/d) = (a * c) / (b * d)
This means you multiply the numerators together and the denominators together. Simplification is often necessary after the multiplication.
Advanced Applications: Algebra and Calculus
The fundamental principles of fractional multiplication are crucial building blocks for more advanced mathematical concepts such as algebra and calculus. Understanding how to manipulate fractions efficiently is essential for solving equations, simplifying expressions, and working with derivatives and integrals.
Conclusion: The Importance of Foundational Math
The simple calculation of 3/4 times 2, although seemingly insignificant on its own, serves as a fundamental stepping stone to a deeper understanding of mathematical principles. Mastering this concept, and the various methods of solving it, lays a solid foundation for tackling more complex mathematical problems in various fields. The ability to work confidently with fractions is a highly valuable skill in numerous academic and professional settings. By understanding the different approaches and their applications, we can appreciate the true significance of this seemingly basic arithmetic problem. It's a testament to how seemingly simple concepts form the cornerstone of broader mathematical understanding and problem-solving.
Latest Posts
Latest Posts
-
5 4 3 2 1 Math Term
May 25, 2025
-
What Is The Greatest Common Factor Of 52 And 78
May 25, 2025
-
What Is The Greatest Common Factor Of 28 And 48
May 25, 2025
-
How Many Miles Will I Drive In A Year Calculator
May 25, 2025
-
Greatest Common Factor Of 14 And 49
May 25, 2025
Related Post
Thank you for visiting our website which covers about How Much Is 3/4 Times 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.