How Much Is 2 3 Plus 2 3
listenit
May 21, 2025 · 5 min read
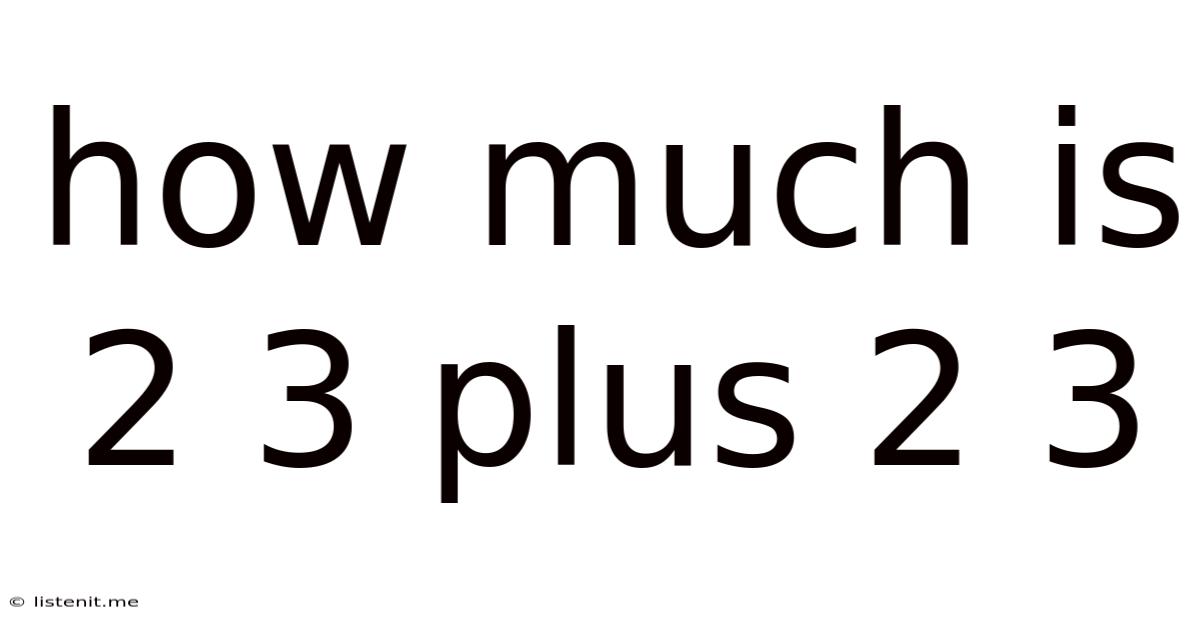
Table of Contents
How Much is 2³ + 2³? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "How much is 2³ + 2³?" opens the door to a fascinating exploration of exponents, their properties, and their widespread applications in various fields. While the immediate answer is straightforward, understanding the underlying principles empowers us to tackle more complex mathematical problems and appreciate the power of exponential growth in the real world.
Understanding Exponents
Before diving into the calculation, let's solidify our understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In the expression 2³, the base is 2, and the exponent is 3. This means 2³ = 2 × 2 × 2 = 8.
Key Terminology:
- Base: The number being multiplied.
- Exponent: The number indicating how many times the base is multiplied by itself.
- Power: Another term for exponent.
Properties of Exponents
Several properties govern how exponents behave. These properties are crucial for simplifying complex expressions and solving equations involving exponents:
- Product of Powers: When multiplying two numbers with the same base, add the exponents: a<sup>m</sup> × a<sup>n</sup> = a<sup>m+n</sup>
- Quotient of Powers: When dividing two numbers with the same base, subtract the exponents: a<sup>m</sup> ÷ a<sup>n</sup> = a<sup>m-n</sup>
- Power of a Power: When raising a power to another power, multiply the exponents: (a<sup>m</sup>)<sup>n</sup> = a<sup>mn</sup>
- Power of a Product: When raising a product to a power, raise each factor to that power: (ab)<sup>n</sup> = a<sup>n</sup>b<sup>n</sup>
- Power of a Quotient: When raising a quotient to a power, raise both the numerator and the denominator to that power: (a/b)<sup>n</sup> = a<sup>n</sup>/b<sup>n</sup>
Calculating 2³ + 2³
Now, let's return to the original question: How much is 2³ + 2³?
First, we calculate each term separately:
- 2³ = 2 × 2 × 2 = 8
Therefore, the expression becomes:
- 8 + 8 = 16
Therefore, 2³ + 2³ = 16.
This simple calculation illustrates the fundamental principles of exponents and arithmetic operations. However, the significance extends far beyond this basic problem.
Applications of Exponents in Real-World Scenarios
The concept of exponents is not confined to theoretical mathematics; it permeates various aspects of our lives, impacting fields such as:
1. Finance and Compound Interest
Exponential growth is vividly exemplified in compound interest calculations. Compound interest involves earning interest not only on the principal amount but also on accumulated interest. The formula for compound interest demonstrates the power of exponents:
A = P(1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
2. Population Growth
Population growth often follows an exponential pattern. In the absence of limiting factors, a population can grow exponentially, doubling or tripling within specific timeframes. Understanding exponential growth models is essential for predicting future population sizes and planning for resource allocation.
3. Radioactive Decay
Conversely, radioactive decay follows an exponential decay pattern. The amount of radioactive material diminishes exponentially over time, with a characteristic half-life—the time it takes for half of the material to decay. This concept is crucial in nuclear physics, medicine (radioactive tracing), and geology (radiometric dating).
4. Computer Science and Data Storage
In computer science, exponents are fundamental to understanding data storage capacities. Terms like kilobytes (KB), megabytes (MB), gigabytes (GB), and terabytes (TB) represent powers of 2 (2<sup>10</sup>, 2<sup>20</sup>, 2<sup>30</sup>, 2<sup>40</sup>, respectively). These powers of 2 reflect the binary nature of computer systems.
5. Scientific Notation
Scientific notation utilizes exponents to represent extremely large or small numbers concisely. For example, the speed of light (approximately 300,000,000 meters per second) can be expressed as 3 x 10<sup>8</sup> m/s. This notation simplifies calculations and improves readability in scientific contexts.
6. Biology and Cell Growth
Cellular processes frequently involve exponential growth or decay. For example, bacterial growth under ideal conditions will show exponential increase in numbers. Conversely, the decay of certain biological compounds can also be described using exponential functions.
Extending the Concept: More Complex Exponential Expressions
While 2³ + 2³ is a simple example, the principles of exponents apply to more complex expressions. For instance:
- (2³)²: This expression involves a power of a power. First, we calculate 2³ (which is 8), and then we square the result: 8² = 64.
- 2³ × 2⁴: This exemplifies the product of powers. We add the exponents: 2<sup>3+4</sup> = 2⁷ = 128.
- 2⁵ / 2²: This involves the quotient of powers. We subtract the exponents: 2<sup>5-2</sup> = 2³ = 8.
Mastering these fundamental properties enables us to simplify and solve even more complex equations involving exponents.
Conclusion: The Enduring Significance of Exponents
The seemingly basic question, "How much is 2³ + 2³?" has led us on a journey into the fascinating world of exponents. While the direct answer is 16, the underlying principles of exponents have far-reaching implications across diverse disciplines. From finance and population growth to computer science and scientific notation, understanding exponents is crucial for navigating complex real-world problems and appreciating the powerful influence of exponential growth and decay. The ability to manipulate and interpret exponential expressions is a valuable skill with broad applicability, extending far beyond the realm of simple mathematical calculations. Continual practice and exploration of these concepts will reinforce your understanding and empower you to tackle even more challenging mathematical problems in the future.
Latest Posts
Latest Posts
-
Average Size Of Spleen In Cm
Jun 05, 2025
-
Pancreas Is Obscured By Overlying Bowel Gas
Jun 05, 2025
-
Natural Remedies For Foot And Mouth Disease
Jun 05, 2025
-
The Internal Scaffolding Of Eukaryotic Cells Is Termed The
Jun 05, 2025
-
The Psychologist Known For Challenging Peoples Absurd Self Defeating Ideas Is
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about How Much Is 2 3 Plus 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.