How Much Is 1/3 Plus 1/3
listenit
May 24, 2025 · 5 min read
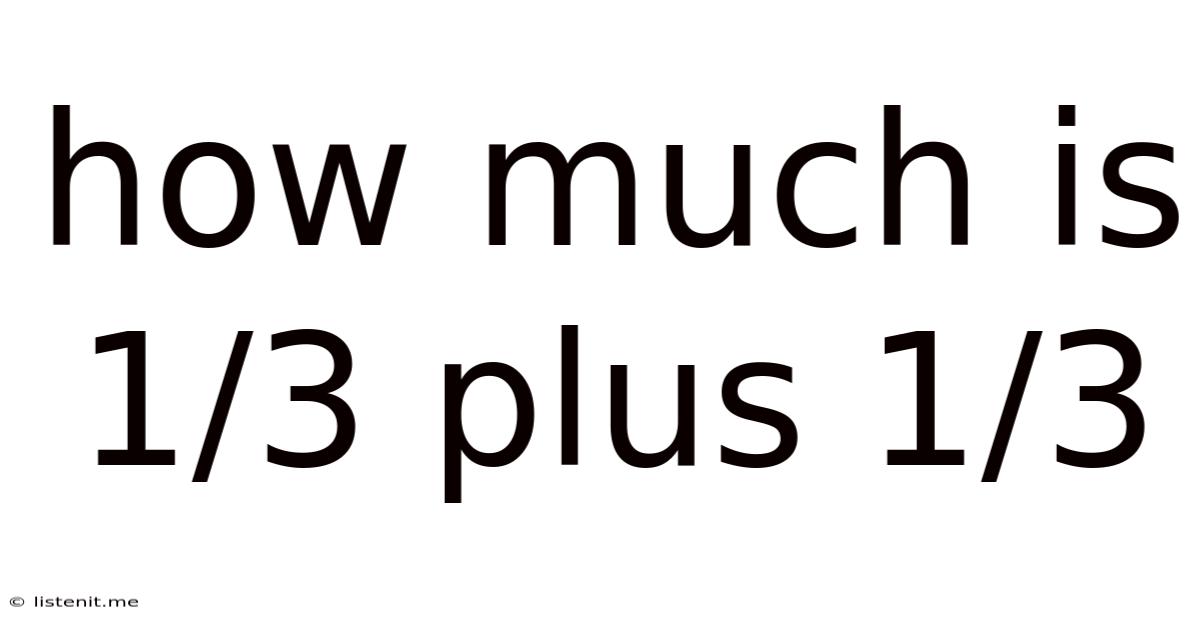
Table of Contents
How Much is 1/3 Plus 1/3? A Deep Dive into Fraction Addition
The seemingly simple question, "How much is 1/3 plus 1/3?" opens the door to a fascinating exploration of fractions, their properties, and their practical applications in various fields. While the answer itself is straightforward for those familiar with basic arithmetic, understanding the underlying principles solidifies fundamental mathematical concepts and provides a solid foundation for more complex calculations. This article will delve into this seemingly simple problem, exploring various methods of solving it and demonstrating its relevance beyond the classroom.
Understanding Fractions: The Building Blocks of Mathematics
Before we tackle the problem at hand, let's revisit the concept of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
In our case, we're dealing with the fraction 1/3. This means the whole is divided into three equal parts, and we're considering one of those parts. Understanding this basic representation is crucial for performing operations with fractions.
Adding Fractions: A Step-by-Step Guide
Adding fractions with the same denominator is remarkably straightforward. The process involves simply adding the numerators while keeping the denominator the same. Let's apply this to our problem:
1/3 + 1/3 = (1 + 1) / 3 = 2/3
Therefore, 1/3 plus 1/3 equals 2/3.
Visualizing the Solution: A Practical Approach
Visual aids can significantly improve understanding, especially when dealing with abstract concepts like fractions. Imagine a pizza cut into three equal slices. Each slice represents 1/3 of the whole pizza. If you take one slice (1/3) and then another slice (1/3), you've taken two slices in total, representing 2/3 of the pizza. This visual representation helps solidify the mathematical concept.
Extending the Concept: Adding Fractions with Different Denominators
While our initial problem involved fractions with the same denominator, it's important to understand how to add fractions with different denominators. This requires finding a common denominator, which is a number that is a multiple of both denominators. Let's consider an example:
1/2 + 1/4
To add these fractions, we need to find a common denominator for 2 and 4. The least common multiple of 2 and 4 is 4. We then convert each fraction to an equivalent fraction with a denominator of 4:
1/2 = 2/4 (multiply both numerator and denominator by 2)
Now we can add:
2/4 + 1/4 = (2 + 1) / 4 = 3/4
Real-World Applications: Where Fractions Matter
Fractions are not confined to the realm of theoretical mathematics; they find widespread application in numerous real-world scenarios:
-
Cooking and Baking: Recipes often call for fractional amounts of ingredients, such as 1/2 cup of flour or 2/3 cup of sugar. Understanding fractions is essential for accurate measurements and successful outcomes.
-
Construction and Engineering: Precise measurements are critical in construction and engineering projects. Fractions are used to represent dimensions, quantities of materials, and angles, ensuring accuracy and structural integrity.
-
Finance and Economics: Fractions are fundamental in finance, used to calculate interest rates, proportions of investments, and analyze financial data.
-
Science and Medicine: Scientific experiments and medical dosages often require precise measurements and calculations involving fractions.
-
Everyday Life: Sharing food, dividing tasks, or understanding discounts often involve fractional calculations.
Beyond the Basics: Exploring More Complex Fraction Operations
Adding fractions is just the beginning. Once you've mastered addition, you can explore other operations, such as:
-
Subtraction of Fractions: Similar to addition, subtracting fractions with the same denominator involves subtracting the numerators while keeping the denominator the same. Subtracting fractions with different denominators requires finding a common denominator before performing the subtraction.
-
Multiplication of Fractions: Multiplying fractions involves multiplying the numerators together and the denominators together.
-
Division of Fractions: Dividing fractions involves inverting (flipping) the second fraction and then multiplying.
Mastering Fractions: Tips and Strategies
-
Practice Regularly: The key to mastering fractions is consistent practice. Work through numerous examples, gradually increasing the complexity of the problems.
-
Visual Aids: Use visual aids, such as diagrams or real-world objects, to help visualize and understand the concepts.
-
Break Down Complex Problems: If you encounter a complex problem, break it down into smaller, more manageable steps.
-
Seek Help When Needed: Don't hesitate to ask for help from a teacher, tutor, or classmate if you're struggling with a particular concept.
The Significance of 1/3 + 1/3 in Advanced Mathematics
While the simple addition of 1/3 + 1/3 seems elementary, the underlying concepts have significant implications in more advanced mathematical fields. For example:
-
Calculus: Understanding fractions is crucial for grasping the concept of limits, derivatives, and integrals, fundamental building blocks of calculus. The ability to manipulate and simplify fractional expressions is essential for solving complex calculus problems.
-
Linear Algebra: Fractions play a vital role in linear algebra, particularly in matrix operations and solving systems of linear equations. Fractional coefficients within matrices necessitate a strong understanding of fractional arithmetic.
-
Probability and Statistics: Fractions are ubiquitous in probability and statistics. Calculating probabilities, representing proportions, and analyzing statistical data often involve fractional representations and calculations.
Conclusion: The Power of Simple Fractions
The seemingly trivial problem of 1/3 + 1/3 reveals a universe of mathematical concepts and practical applications. While the answer itself is simple (2/3), the journey to understanding the underlying principles strengthens fundamental mathematical skills and builds a strong foundation for tackling more complex calculations. From cooking to engineering, finance to science, fractions are an integral part of our daily lives, making their mastery an invaluable asset. By embracing practice, visualization, and a willingness to explore, you can confidently navigate the world of fractions and unlock their immense potential. Remember, the power of mathematics lies in its ability to explain and solve problems within the fabric of our world, starting with the seemingly simple addition of fractions.
Latest Posts
Latest Posts
-
20 Divided By 3 In Fraction
May 24, 2025
-
How Much Taxes On 401k Withdrawal Calculator
May 24, 2025
-
30 Days From January 16th 2024
May 24, 2025
-
How To Calculate 5 Of A Number
May 24, 2025
-
How To Maximize Employer 401k Match Calculator
May 24, 2025
Related Post
Thank you for visiting our website which covers about How Much Is 1/3 Plus 1/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.