How Many Lines Of Symmetry Does A Heptagon Have
listenit
Mar 29, 2025 · 5 min read
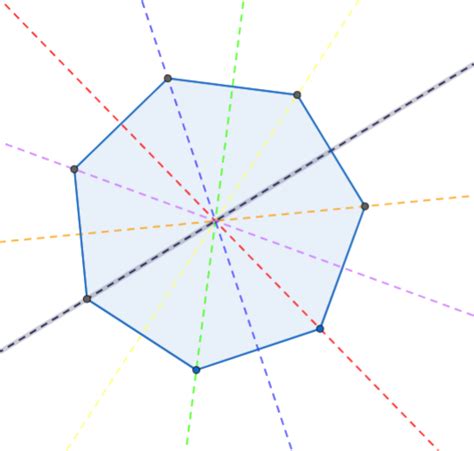
Table of Contents
How Many Lines of Symmetry Does a Heptagon Have? Exploring Symmetry in Regular and Irregular Heptagons
The question of how many lines of symmetry a heptagon possesses is a fascinating exploration into the world of geometry and symmetry. While seemingly simple, understanding the answer requires a grasp of fundamental geometric concepts and a clear distinction between regular and irregular heptagons. This article delves deep into this topic, providing a comprehensive explanation suitable for students, educators, and anyone interested in the beauty of mathematical shapes.
Understanding Symmetry and Lines of Symmetry
Before diving into the specifics of heptagons, let's establish a clear understanding of symmetry and lines of symmetry. Symmetry, in its simplest form, refers to a balanced arrangement of parts or features within a shape. A shape is considered symmetrical if it can be folded or rotated in such a way that one half exactly mirrors the other. A line of symmetry (also known as an axis of symmetry) is a line that divides a shape into two identical halves, such that folding the shape along this line would result in perfect overlap.
The Case of the Regular Heptagon
A regular heptagon is a seven-sided polygon with all sides of equal length and all interior angles of equal measure. This regularity is crucial in determining the number of lines of symmetry. Unlike simpler polygons like squares or equilateral triangles, the symmetry of a regular heptagon is less intuitive.
To determine the lines of symmetry, imagine folding a regular heptagon. Each line of symmetry must bisect (cut in half) the heptagon, creating two congruent halves. A key to understanding this is recognizing that every line of symmetry must connect a vertex (corner) to the midpoint of the opposite side. In a regular polygon, the number of lines of symmetry is equal to the number of sides.
Therefore, a regular heptagon, having seven sides, possesses seven lines of symmetry. These seven lines radiate from the center of the heptagon, each connecting a vertex to the midpoint of the opposite side. These lines act as axes of reflectional symmetry. You can visualize this by mentally folding the heptagon along each of these lines; each fold results in a perfect mirror image.
Visualizing the Lines of Symmetry in a Regular Heptagon
Imagine a perfect, equally-sided heptagon drawn on a piece of paper. To visualize the seven lines of symmetry:
-
Connect each vertex to the midpoint of the opposite side. This is the simplest way to identify the lines of symmetry. Note that, unlike some other polygons, the lines of symmetry do not connect vertices to other vertices.
-
Draw a line through the center of the heptagon, extending from one vertex to the midpoint of the opposite side. Repeat this process for each vertex.
-
Observe that there are seven lines in total. These are your lines of symmetry.
The Case of the Irregular Heptagon
An irregular heptagon is a seven-sided polygon where the sides and angles are not all equal. Unlike its regular counterpart, an irregular heptagon will generally have fewer lines of symmetry, or even no lines of symmetry at all. The absence or presence of symmetry is highly dependent on the specific arrangement of its sides and angles.
Determining the lines of symmetry in an irregular heptagon requires a more careful, case-by-case approach. There's no simple formula to apply, as the number of lines of symmetry (if any) will vary drastically based on the shape's configuration.
Examples of Irregular Heptagons and Their Symmetry
Let's consider a few scenarios to illustrate this:
-
Irregular Heptagon with One Line of Symmetry: It's possible to construct an irregular heptagon with exactly one line of symmetry. This line would divide the heptagon into two mirror images. The rest of the polygon would not exhibit any further symmetry.
-
Irregular Heptagon with No Lines of Symmetry: Most irregular heptagons will not possess any lines of symmetry at all. This is because any attempt to divide the polygon into two identical halves will be unsuccessful.
-
Irregular Heptagon with Two or More Lines of Symmetry: Extremely rare, and typically only occurring due to specific and improbable combinations of side and angle lengths.
Analyzing Symmetry in Irregular Heptagons
To analyze the symmetry of an irregular heptagon, consider these steps:
-
Visual Inspection: Start by visually inspecting the heptagon. Look for any potential lines that might divide it into two symmetrical halves.
-
Paper Folding: If a physical representation exists, attempt to fold the heptagon along different lines. If a fold results in perfect overlap, you’ve found a line of symmetry.
-
Geometric Software: If you're working with digital representations of heptagons, various geometric software packages allow for precise measurements and symmetry checks, simplifying the process.
Rotational Symmetry: A Related Concept
While we've focused on lines of symmetry (also called reflectional symmetry), it's important to briefly mention rotational symmetry. This refers to a shape's ability to appear unchanged after being rotated about a central point. A regular heptagon possesses rotational symmetry of order 7, meaning it looks identical after being rotated through an angle of 360°/7 ≈ 51.43°. Irregular heptagons may or may not exhibit rotational symmetry, depending on their specific shape.
Heptagons in Real-World Applications
Understanding heptagons and their symmetry is not just an academic exercise. Heptagons, although less common than other polygons, appear in various real-world applications, though often not as perfectly regular shapes:
-
Certain Crystals: Some naturally occurring crystals exhibit heptagonal shapes.
-
Architecture and Design: Although less frequent than triangles, squares, and hexagons, heptagonal shapes can be found in certain architectural designs and artistic creations.
-
Man-Made Objects: Various manufactured objects may incorporate heptagonal elements, though imperfections may render perfect symmetry irrelevant in practical contexts.
Conclusion: A Deeper Understanding of Heptagonal Symmetry
The number of lines of symmetry in a heptagon is directly tied to its regularity. A regular heptagon boasts seven lines of symmetry, while irregular heptagons can have fewer, or even zero. This exploration highlights the importance of understanding the relationship between geometric properties and symmetry. By carefully analyzing the arrangement of sides and angles, we can determine the degree of symmetry present in any given heptagon, be it regular or irregular. This knowledge extends beyond pure geometry, finding applications in various fields such as crystallography, architecture, and design. The seemingly simple question of heptagonal symmetry opens a door to a broader understanding of geometric concepts and their practical implications.
Latest Posts
Latest Posts
-
Is Wood Rotting A Physical Or Chemical Change
Mar 31, 2025
-
1 Lb Equals How Many Pints
Mar 31, 2025
-
What Is The Mass Of 5 Moles Of Fe2o3
Mar 31, 2025
-
1 X 2 1 X 3
Mar 31, 2025
-
What Is 90 As A Fraction
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about How Many Lines Of Symmetry Does A Heptagon Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
