How Many 2 5 Are In 2
listenit
May 24, 2025 · 5 min read
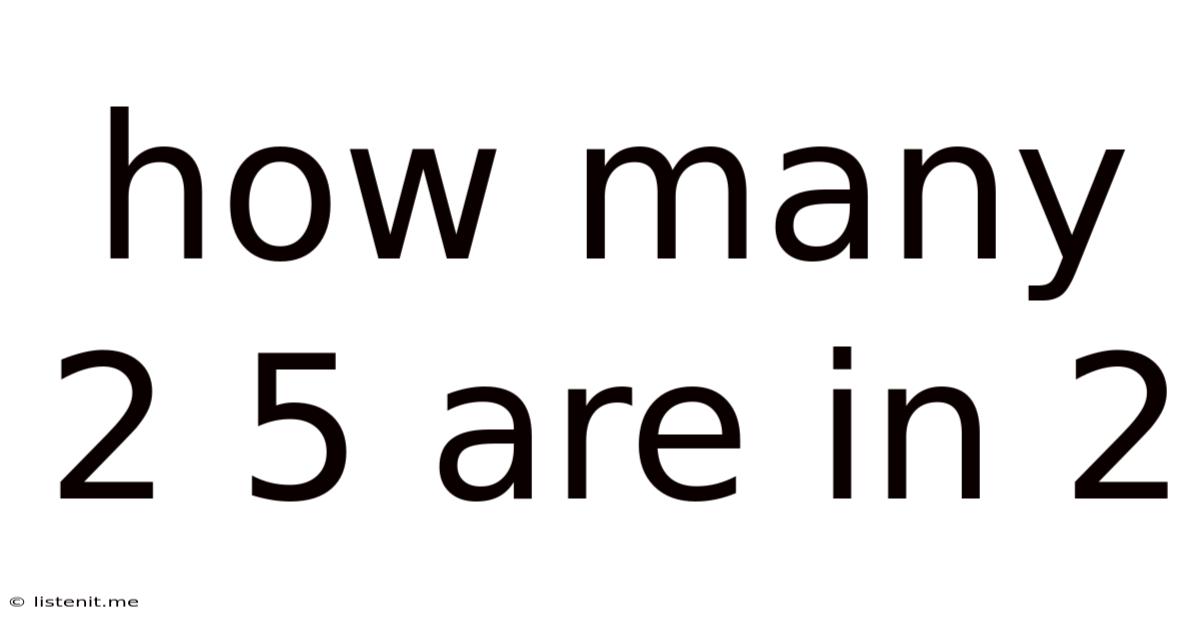
Table of Contents
How Many 2/5s Are in 2? A Deep Dive into Fraction Division
The question, "How many 2/5s are in 2?" might seem deceptively simple at first glance. It's a fundamental concept in mathematics, dealing with fraction division, a skill crucial for various applications from baking to engineering. This article will explore this question thoroughly, going beyond the simple answer to explain the underlying principles and provide practical applications. We'll explore different methods of solving this problem, solidify the understanding with examples, and delve into the broader context of fraction manipulation.
Understanding the Problem: A Conceptual Approach
Before jumping into calculations, let's visualize the problem. Imagine you have two whole pies. Each piece represents 2/5 of a pie. The question is essentially asking: how many of these 2/5-sized pieces can you cut from two whole pies? This visual representation makes the problem more intuitive and less abstract.
Method 1: Converting to Improper Fractions
One common approach to solving this problem involves converting the whole number (2) into an improper fraction with the same denominator as the fraction (2/5). This allows for straightforward division.
-
Step 1: Convert 2 to a fraction with a denominator of 5. Since 2 is equivalent to 10/5 (2 x 5/5 = 10/5), we now have the problem: 10/5 ÷ 2/5.
-
Step 2: Invert and multiply. The rule for dividing fractions is to invert (flip) the second fraction and then multiply. This gives us: 10/5 x 5/2.
-
Step 3: Simplify and solve. Multiply the numerators (10 x 5 = 50) and the denominators (5 x 2 = 10). This results in 50/10. Simplifying this fraction by dividing both the numerator and the denominator by 10, we get the answer: 5.
Therefore, there are 5 pieces of size 2/5 in 2.
Method 2: Using Reciprocal and Multiplication
This method utilizes the concept of reciprocals. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/5 is 5/2. This method streamlines the process.
-
Step 1: Find the reciprocal of 2/5. The reciprocal is 5/2.
-
Step 2: Multiply the whole number by the reciprocal. This gives us: 2 x 5/2.
-
Step 3: Simplify and solve. The 2 in the numerator and the 2 in the denominator cancel each other out, leaving 5.
This method directly yields the answer: 5. This approach emphasizes the core concept of division as the inverse of multiplication.
Method 3: Visual Representation and Repeated Subtraction
This method provides a more intuitive understanding of the problem, particularly helpful for visualizing fraction division.
Imagine you have two whole pies. You're cutting them into pieces, each representing 2/5 of a pie. Let's repeatedly subtract 2/5 from the total amount (2) until we reach zero.
- First subtraction: 2 - 2/5 = 1 3/5
- Second subtraction: 1 3/5 - 2/5 = 1 1/5
- Third subtraction: 1 1/5 - 2/5 = 4/5
- Fourth subtraction: 4/5 - 2/5 = 2/5
- Fifth subtraction: 2/5 - 2/5 = 0
We have subtracted 2/5 a total of five times before reaching zero. This method reinforces the concept of division as repeated subtraction.
Real-World Applications of Fraction Division
Understanding fraction division isn't just an academic exercise; it has widespread practical applications in numerous fields:
-
Cooking and Baking: Recipes often require fractional measurements. If a recipe calls for 2/5 of a cup of flour and you want to double the recipe, you need to figure out how many 2/5 cups are in 2 cups.
-
Construction and Engineering: Dividing lengths, calculating material quantities, and determining proportions are crucial aspects of construction and engineering, often involving fraction division.
-
Finance and Economics: Calculating percentages, shares, and proportions of investments frequently involves working with fractions.
-
Data Analysis and Statistics: When working with datasets involving fractions or ratios, dividing fractions is a fundamental step in analysis and interpretation.
-
Sewing and Crafting: Calculating fabric yardage, bead quantities, or other crafting materials often requires working with fractional measurements and divisions.
Extending the Concept: Solving Similar Problems
Let's extend our understanding by tackling similar problems:
Problem 1: How many 3/7s are in 3?
Using the method of converting to improper fractions:
- Convert 3 to a fraction with a denominator of 7: 21/7
- Divide 21/7 by 3/7: 21/7 x 7/3 = 7
Therefore, there are 7 pieces of size 3/7 in 3.
Problem 2: How many 1/4s are in 2 1/2?
- Convert 2 1/2 to an improper fraction: 5/2
- Divide 5/2 by 1/4: 5/2 x 4/1 = 10
Therefore, there are 10 pieces of size 1/4 in 2 1/2.
These examples showcase the adaptability of the methods discussed earlier to various fraction division problems.
Troubleshooting Common Mistakes
Students often encounter difficulties when dealing with fraction division. Some common mistakes to avoid include:
-
Incorrectly inverting the fraction: Remember to invert only the second fraction (the divisor) when dividing fractions.
-
Not simplifying the fraction: Always simplify the final answer to its lowest terms.
-
Incorrect multiplication of fractions: Ensure you correctly multiply the numerators and denominators separately.
-
Failing to convert mixed numbers to improper fractions: Before dividing, convert any mixed numbers to improper fractions for easier calculation.
Conclusion: Mastering Fraction Division
The seemingly simple question, "How many 2/5s are in 2?" opens the door to understanding the fundamental concept of fraction division. By mastering different methods – converting to improper fractions, using reciprocals, and visualizing through repeated subtraction – you not only solve this specific problem but also develop a solid foundation for tackling more complex fraction manipulations. The practical applications of this skill extend across numerous disciplines, highlighting the importance of mastering this crucial mathematical concept. Remember to practice regularly and identify potential pitfalls to become proficient in fraction division. Through consistent practice and understanding, you can confidently tackle fraction problems and apply them to real-world scenarios.
Latest Posts
Latest Posts
-
1 6 To The Power Of 2 As A Fraction
May 24, 2025
-
Greatest Common Factor Of 60 And 80
May 24, 2025
-
What Is 75 Percent Of 10
May 24, 2025
-
How Many Weight Watchers Points In Honey
May 24, 2025
-
Whats The Prime Factorization Of 64
May 24, 2025
Related Post
Thank you for visiting our website which covers about How Many 2 5 Are In 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.