How Many 1/5 Are In 3
listenit
May 26, 2025 · 4 min read
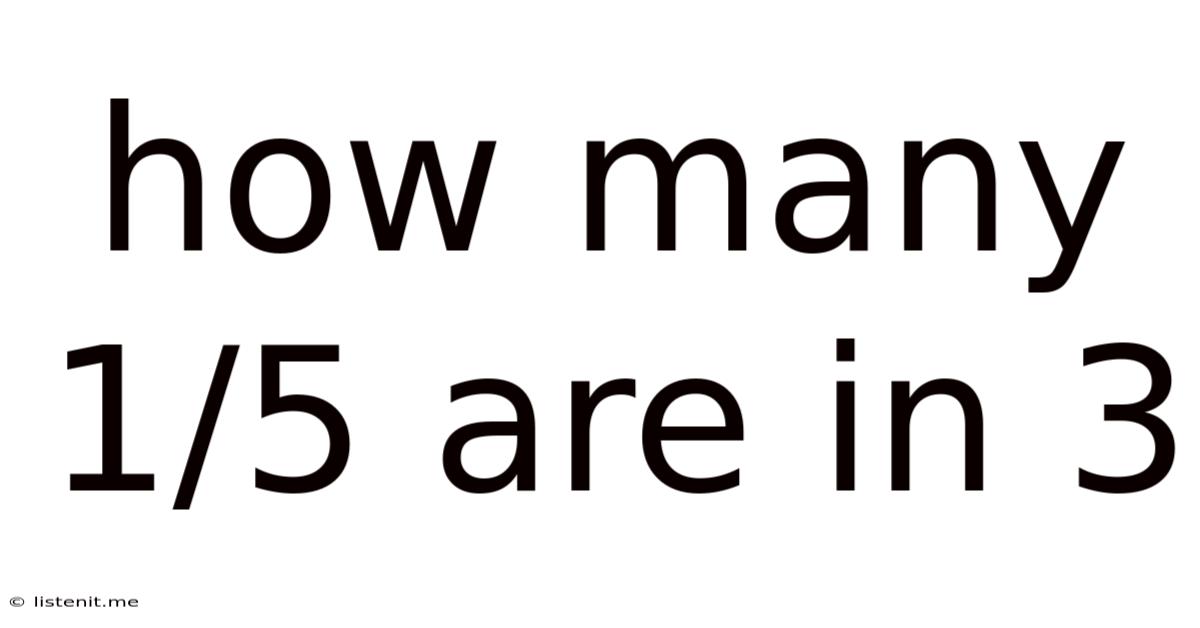
Table of Contents
How Many 1/5s Are in 3? A Deep Dive into Fractions and Division
This seemingly simple question, "How many 1/5s are in 3?", opens a door to a deeper understanding of fractions, division, and their practical applications. While the answer might seem immediately obvious to some, exploring the various ways to solve this problem illuminates fundamental mathematical concepts crucial for both basic arithmetic and more advanced studies. This article will provide a comprehensive exploration of this question, examining different approaches, illustrating the concepts with real-world examples, and emphasizing the importance of understanding fractional relationships.
Understanding the Question: Fractions and Division
The question "How many 1/5s are in 3?" is essentially asking us to perform division. We're dividing the whole number 3 by the fraction 1/5. This is equivalent to asking, "How many times does 1/5 go into 3?"
Understanding fractions is key here. A fraction represents a part of a whole. The fraction 1/5 means one out of five equal parts. Imagine a pizza cut into five slices; 1/5 represents one slice. The question then becomes: how many of these single slices (1/5) are there in three whole pizzas?
Method 1: Using Reciprocal Multiplication
The most efficient method to solve this problem is to use the reciprocal of the fraction. The reciprocal of a fraction is obtained by switching the numerator and the denominator. The reciprocal of 1/5 is 5/1, or simply 5.
To divide by a fraction, we multiply by its reciprocal. Therefore, the problem "3 ÷ 1/5" becomes:
3 × 5 = 15
Therefore, there are 15 one-fifths in 3.
Method 2: Visual Representation
Visualizing the problem can be incredibly helpful, especially for beginners. Imagine three whole bars representing the number 3. Now, divide each bar into five equal parts, representing the 1/5 fractions.
[Imagine three bars divided into five equal sections here. Unfortunately, I can't create visual images within this text-based format.]
Counting the total number of 1/5 sections across all three bars will give you the answer: 15. This visual approach reinforces the concept of fractions and division in a concrete way.
Method 3: Converting to a Common Denominator
Another method involves converting the whole number 3 into a fraction with a denominator of 5. Since 3 can be written as 3/1, we find an equivalent fraction with a denominator of 5:
3/1 = (3 × 5) / (1 × 5) = 15/5
Now the question becomes: how many 1/5s are in 15/5? This is simply 15 ÷ 1 = 15. Again, we arrive at the answer of 15.
Real-World Applications: Putting it into Practice
The concept of dividing whole numbers by fractions is prevalent in many real-world scenarios. Consider the following examples:
-
Baking: A recipe calls for 1/5 cup of sugar per batch of cookies. How many batches can you make with 3 cups of sugar? The answer, as we've established, is 15 batches.
-
Construction: A project requires pieces of wood that are 1/5 of a meter long. How many pieces can you cut from a 3-meter long plank? Again, you can get 15 pieces.
-
Fabric: You have 3 meters of fabric, and each garment requires 1/5 of a meter. How many garments can you make? You can make 15 garments.
These examples demonstrate the practical significance of understanding fractional division in everyday life.
Extending the Concept: More Complex Fractions
The principle of dividing by fractions extends to more complex scenarios. For instance, consider the question: "How many 2/5s are in 3?"
Following the reciprocal method:
3 ÷ 2/5 = 3 × 5/2 = 15/2 = 7.5
This demonstrates that there are 7.5 two-fifths in 3.
Importance of Understanding Fractions in Mathematics
Understanding fractions is a foundational element in mathematics. It forms the basis for:
-
Decimals: Fractions can be easily converted to decimals, and vice-versa. This conversion is essential for various calculations and applications.
-
Algebra: Solving algebraic equations often involves working with fractions and understanding their properties.
-
Calculus: Advanced mathematical concepts like calculus heavily rely on a strong understanding of fractions and limits.
-
Geometry: Calculations involving areas, volumes, and proportions often involve fractions.
Mastering fractions is not just about solving simple problems; it's about developing a strong foundation for more advanced mathematical concepts.
Conclusion: Mastering Fractions for a Stronger Mathematical Foundation
The seemingly simple question of "How many 1/5s are in 3?" provides a gateway to a deeper exploration of fractional division and its wide-ranging applications. Through various methods – using reciprocals, visual representation, and converting to common denominators – we've demonstrated that there are 15 one-fifths in 3. The importance of understanding fractions extends far beyond elementary arithmetic, forming a crucial foundation for success in more advanced mathematical studies and real-world problem-solving. By mastering fractions, you equip yourself with a valuable tool for navigating various mathematical and practical challenges. Remember, consistent practice and a thorough understanding of the underlying principles are key to achieving proficiency in this fundamental area of mathematics. The more you engage with these concepts, the more intuitive and effortless they will become.
Latest Posts
Latest Posts
-
What Is 32 As A Fraction
May 26, 2025
-
Least Common Multiple Of 12 And 22
May 26, 2025
-
What Is 9 Months Before January 21
May 26, 2025
-
What Is 9 As A Fraction
May 26, 2025
-
4 Out Of 16 Is What Percent
May 26, 2025
Related Post
Thank you for visiting our website which covers about How Many 1/5 Are In 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.