How Many 1 3 Cups Make 1 2 Cup
listenit
May 12, 2025 · 5 min read
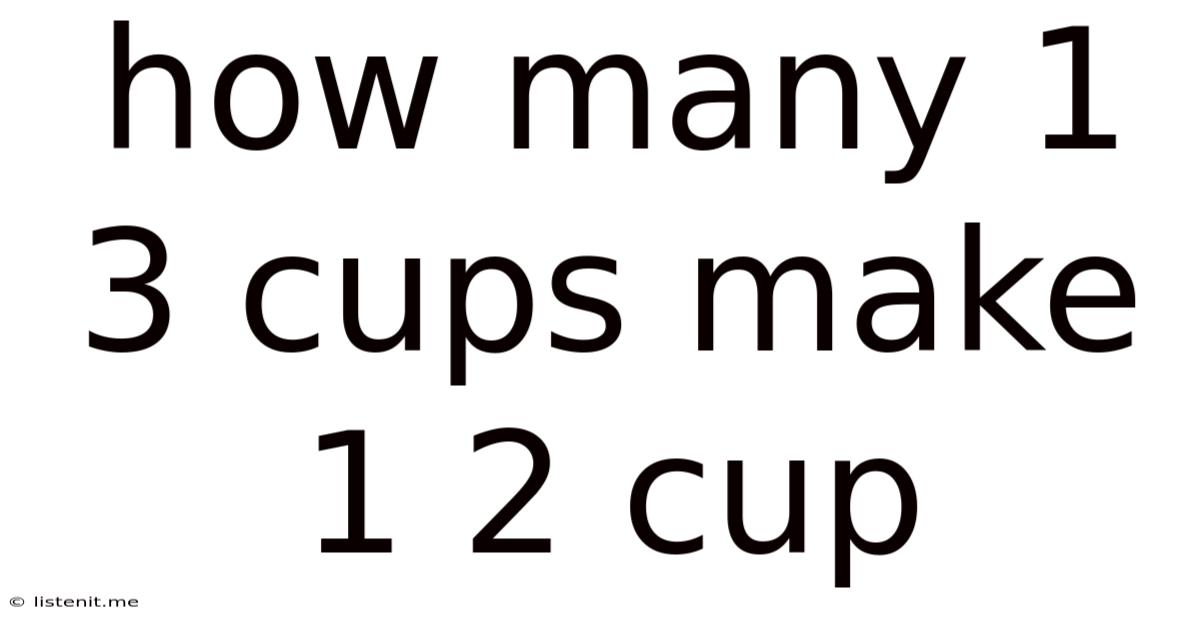
Table of Contents
How Many 1/3 Cups Make 1/2 Cup? A Comprehensive Guide to Fraction Conversions in Cooking
Understanding fractions is crucial in many aspects of life, but it's especially important in cooking and baking. Precise measurements are key to achieving the desired texture and taste in your culinary creations. One common question that arises frequently is: how many 1/3 cups make 1/2 a cup? This seemingly simple question opens the door to a broader understanding of fraction manipulation and its applications in everyday scenarios. This comprehensive guide will not only answer this question but also provide you with the tools and knowledge to tackle similar fraction conversions with confidence.
Deciphering the Question: 1/3 Cups vs. 1/2 Cup
The core question – "How many 1/3 cups make 1/2 cup?" – is essentially asking us to solve a simple division problem involving fractions. We need to determine how many times 1/3 goes into 1/2. While this might seem daunting at first, it’s straightforward once you understand the process of dividing fractions.
Understanding Fraction Division
Dividing fractions involves a clever trick: we flip (or invert) the second fraction (the divisor) and then multiply. This method is often remembered by the phrase "invert and multiply." So, to solve our problem, we'll convert the division problem into a multiplication problem:
1/2 ÷ 1/3 = 1/2 * 3/1
The Calculation: Step-by-Step
-
Invert the second fraction: The second fraction, 1/3, becomes 3/1 (or simply 3).
-
Multiply the numerators: Multiply the top numbers (numerators) together: 1 * 3 = 3
-
Multiply the denominators: Multiply the bottom numbers (denominators) together: 2 * 1 = 2
-
Simplify the result: The result is 3/2. This is an improper fraction (where the numerator is larger than the denominator). To convert it to a mixed number (a whole number and a fraction), we divide the numerator (3) by the denominator (2): 3 ÷ 2 = 1 with a remainder of 1. Therefore, 3/2 is equivalent to 1 1/2.
The Answer: 1 and 1/2
So, the answer to the question "How many 1/3 cups make 1/2 cup?" is 1 1/2. This means you need one and a half 1/3 cups to equal one-half cup.
Practical Applications in Cooking
Understanding this conversion is invaluable in cooking and baking. Imagine you have a recipe that calls for 1/2 cup of flour, but your only measuring cup is a 1/3 cup measure. Knowing that 1 1/2 (1/3) cups equals 1/2 cup allows you to accurately measure the flour without needing a 1/2 cup measuring cup. You simply fill the 1/3 cup measure once completely and then fill it again halfway to obtain the required amount.
Beyond the Basics: Expanding Fraction Knowledge
While the initial question focused on a specific fraction conversion, the underlying principles apply to a wide range of similar problems. Let's explore some related concepts that build upon our understanding:
Converting Fractions to Decimals
Sometimes, working with decimals is easier than fractions. We can easily convert 1/3 and 1/2 into decimals:
- 1/2 = 0.5
- 1/3 = 0.333... (a repeating decimal)
This conversion can be helpful when using digital kitchen scales or working with recipes that use decimal measurements.
Working with Other Fractions
The "invert and multiply" method applies to all fraction divisions. For instance, if your recipe requires 2/3 cup of sugar and you only have a 1/4 cup measuring cup, you can use the same technique:
2/3 ÷ 1/4 = 2/3 * 4/1 = 8/3 = 2 2/3
You would need 2 and 2/3 (1/4) cups of sugar.
Using Proportions
Proportions offer another approach to solving these types of problems. A proportion sets up an equivalence between two ratios. For our original problem, we can write:
x / (1/2) = (1/3) / 1
Solving for x (the number of 1/3 cups), we get:
x = (1/2) * (1/3) = 1/6
This approach, however, gives the incorrect answer. The problem lies in the way the proportion is set up here. A correct proportion would set up the ratio of cups to cups:
(1/3) / x = (1/2) / 1
Solving this proportion gives the correct answer, x = 2/3. There's a subtle but crucial difference in how proportions should be applied here. While it's theoretically possible to solve this using proportions, the method of inverting and multiplying is generally more straightforward and less prone to errors for this specific problem type.
Troubleshooting Common Fraction Errors
Even experienced cooks can sometimes make mistakes with fractions. Here are a few common errors to watch out for:
-
Incorrectly Inverting the Fraction: Remember to invert only the divisor (the fraction you are dividing by).
-
Forgetting to Simplify: Always simplify your final answer to the lowest terms.
-
Mixing Up Numerators and Denominators: Double-check your multiplication to avoid errors.
Conclusion: Mastering Fraction Conversions in Cooking
Mastering fraction conversions significantly improves your cooking and baking skills. By understanding the principles of fraction division and applying the "invert and multiply" method, you can accurately measure ingredients regardless of the measuring cups available. This knowledge empowers you to follow recipes with precision and consistently achieve delicious results. Remember to practice, and you'll soon find yourself confidently tackling fraction conversions in all your culinary endeavors! This skill isn't just about cooking; it's about developing a stronger mathematical foundation applicable in many facets of life. So, the next time you’re in the kitchen, remember this guide and enjoy the confidence that comes with accurately measuring your ingredients!
Latest Posts
Latest Posts
-
Difference Between Molar Mass And Molecular Mass
May 12, 2025
-
632 8 Nm Wavelength Of Red Light From Helium Neon Laser
May 12, 2025
-
Is Organic Layer On Top Or Bottom
May 12, 2025
-
Ionic Compounds Are Composed Of What Particles
May 12, 2025
-
What Is 3 33333 As A Fraction
May 12, 2025
Related Post
Thank you for visiting our website which covers about How Many 1 3 Cups Make 1 2 Cup . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.