How Many 1/3 Cup In 1/2 Cup
listenit
May 10, 2025 · 5 min read
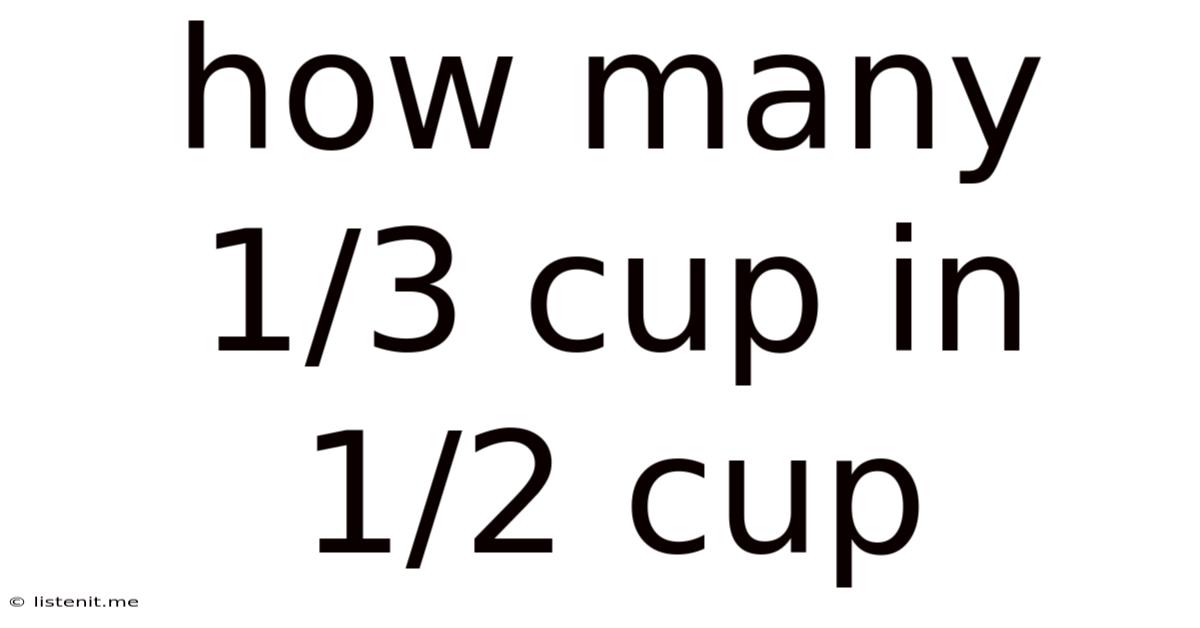
Table of Contents
How Many 1/3 Cups in 1/2 Cup? A Comprehensive Guide to Fraction Conversions
This seemingly simple question, "How many 1/3 cups are in 1/2 cup?", can actually unlock a deeper understanding of fractions and their practical applications in everyday life, especially in cooking and baking. While a quick calculation might suffice for some, let's delve into this topic thoroughly, exploring various methods of solving this problem and expanding on the broader concepts involved. This comprehensive guide will not only answer the question but also equip you with the knowledge to tackle similar fraction conversions with confidence.
Understanding the Fundamentals: Fractions in a Nutshell
Before we dive into the specifics of converting 1/2 cup to 1/3 cups, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key elements:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In our case, we're dealing with 1/2 (one-half) and 1/3 (one-third). 1/2 means one out of two equal parts, while 1/3 represents one out of three equal parts. Understanding this fundamental concept is crucial for mastering fraction conversions.
Method 1: The Direct Conversion Approach
The most straightforward way to determine how many 1/3 cups are in 1/2 cup is through direct division. We essentially want to find out how many times 1/3 fits into 1/2. This can be expressed as a division problem:
(1/2) / (1/3)
To divide fractions, we multiply the first fraction by the reciprocal of the second fraction. The reciprocal of a fraction is simply flipping the numerator and the denominator. The reciprocal of 1/3 is 3/1 (or simply 3). Therefore, our equation becomes:
(1/2) * (3/1) = 3/2
This result, 3/2, means there are 3/2 (or one and a half) 1/3 cups in 1/2 cup.
Method 2: Finding a Common Denominator
Another approach involves finding a common denominator for both fractions. A common denominator is a number that both denominators (2 and 3) can divide into evenly. The least common denominator (LCD) for 2 and 3 is 6.
Let's convert both fractions to have a denominator of 6:
- 1/2 = (1/2) * (3/3) = 3/6
- 1/3 = (1/3) * (2/2) = 2/6
Now we can compare the fractions: How many times does 2/6 fit into 3/6? The answer is 1.5 (or 3/2) times. This confirms our previous result.
Method 3: Visual Representation
Visualizing the problem can be helpful, particularly for those who find abstract mathematical concepts challenging. Imagine a cup divided into six equal parts.
- 1/2 cup: This represents three out of the six parts.
- 1/3 cup: This represents two out of the six parts.
By comparing the two, it's visually evident that 1/2 cup (3/6) contains 1.5 times the amount of a 1/3 cup (2/6).
Practical Applications: Cooking and Baking
Understanding fraction conversions is incredibly useful in cooking and baking. Recipes often require precise measurements, and the ability to convert between different units is essential for achieving consistent results. For instance, if a recipe calls for 1/2 cup of flour, but you only have a 1/3 cup measuring cup, you now know that you need to use the 1/3 cup measuring cup one and a half times.
Beyond the Basics: Expanding Your Fraction Skills
This exercise of converting 1/2 cup to 1/3 cups provides a solid foundation for tackling more complex fraction problems. Mastering fraction conversions opens doors to more advanced mathematical concepts and problem-solving scenarios.
Here are some areas where this skill proves beneficial:
- More complex recipe conversions: Recipes may involve various fractional measurements, requiring multiple conversions to ensure accuracy.
- Building measurements: This skill is crucial when building or constructing items where precise measurements are critical.
- Data analysis: Understanding fractions is essential when interpreting data presented in fractions or percentages.
- Financial calculations: Fraction conversions are frequently used in financial calculations, such as calculating interest rates or portions of investments.
Troubleshooting Common Fraction Conversion Errors
While fraction conversions might seem straightforward, certain errors can occur. Let's address some common pitfalls:
- Incorrect Reciprocal: When dividing fractions, remember to use the reciprocal of the second fraction. Forgetting this crucial step will lead to an incorrect answer.
- Improper Simplification: Always simplify your final answer to its lowest terms. For instance, 6/12 should be simplified to 1/2.
- Incorrect Common Denominator: When finding a common denominator, ensure you select the correct one. Using an incorrect common denominator will lead to inaccurate results.
Conclusion: Mastering Fractions for Everyday Life
The question, "How many 1/3 cups in 1/2 cup?", while simple on the surface, provides a valuable opportunity to reinforce our understanding of fractions and their practical applications. Whether you're a seasoned baker or simply seeking to improve your mathematical skills, mastering fraction conversions is a valuable asset. By understanding the different methods of conversion, from direct division to finding common denominators, and by being aware of potential errors, you can confidently tackle similar problems and enhance your problem-solving abilities in various aspects of your life. Remember, practice makes perfect! The more you work with fractions, the more intuitive and comfortable these calculations will become.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 25 And 15
May 10, 2025
-
Difference Between Core And Valence Electrons
May 10, 2025
-
Why Do Cells Spend Most Of Their Time In Interphase
May 10, 2025
-
29 Degrees Celsius Converted To Fahrenheit
May 10, 2025
-
Difference Between Metal Non Metal And Metalloids
May 10, 2025
Related Post
Thank you for visiting our website which covers about How Many 1/3 Cup In 1/2 Cup . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.