How Many 1/3 Are In 6
listenit
May 12, 2025 · 5 min read
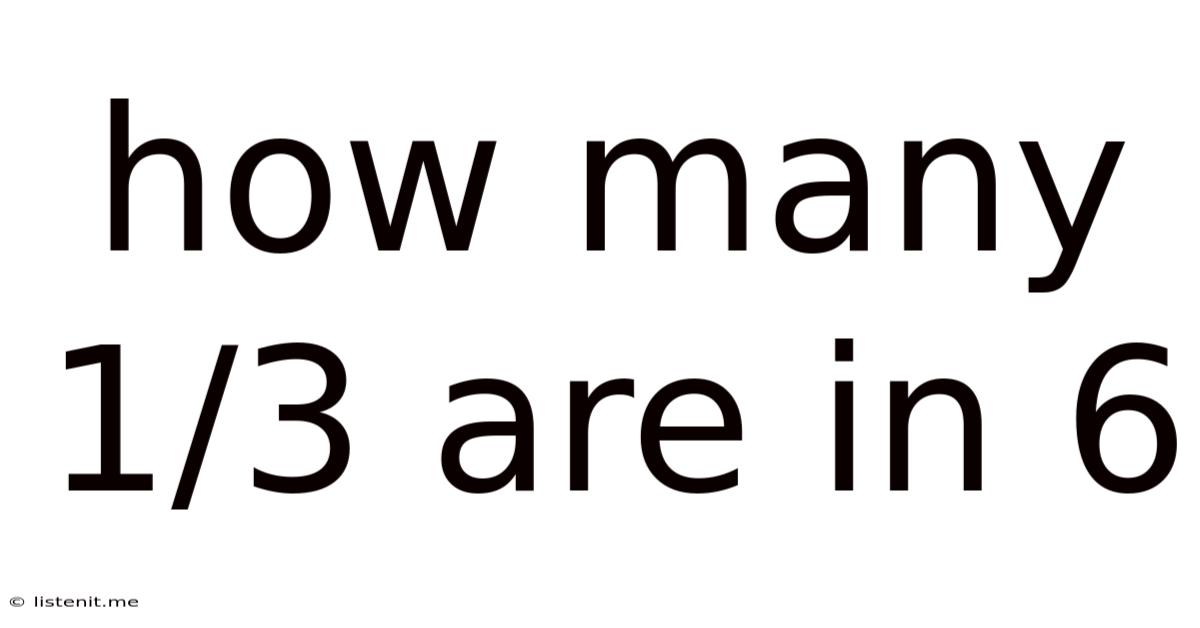
Table of Contents
How Many 1/3s Are in 6? A Deep Dive into Fractions and Division
This seemingly simple question, "How many 1/3s are in 6?", opens the door to a fascinating exploration of fractions, division, and the fundamental principles of mathematics. While the answer might seem immediately obvious to some, a deeper understanding of the underlying concepts reveals a wealth of knowledge applicable to more complex mathematical problems. This article will not only provide the answer but also dissect the various methods of solving this problem, explaining the reasoning behind each approach and its broader implications.
Understanding the Question: Fractions and Division
The question "How many 1/3s are in 6?" is essentially asking us to perform a division. We're dividing the whole number 6 by the fraction 1/3. This can be represented mathematically as:
6 ÷ (1/3)
This expression highlights the core concept: we want to determine how many times the fraction 1/3 fits into the whole number 6. Understanding this phrasing is crucial for selecting the appropriate method of solution.
Method 1: Reciprocal Multiplication
The most efficient way to divide by a fraction is to multiply by its reciprocal. The reciprocal of a fraction is simply the fraction inverted. The reciprocal of 1/3 is 3/1, or simply 3. Therefore, our equation transforms into:
6 x (3/1) = 6 x 3 = 18
Therefore, there are 18 one-thirds in 6.
This method leverages the fundamental property of fractions and division. Dividing by a fraction is equivalent to multiplying by its reciprocal. This simplifies the calculation and makes it easily understandable, even for those less familiar with advanced mathematical concepts.
Visualizing the Solution
Imagine a pie cut into three equal slices. Each slice represents 1/3 of the pie. If you have six whole pies, how many of these 1/3 slices can you get? You can get three slices from each pie, and since you have six pies, you have 6 x 3 = 18 slices. This visual representation reinforces the mathematical solution.
Method 2: Converting to a Common Denominator
Another approach involves converting the whole number 6 into a fraction with the same denominator as 1/3. We can express 6 as 6/1. To find a common denominator, we multiply the numerator and denominator of 6/1 by 3:
6/1 x 3/3 = 18/3
Now, we can compare the two fractions: 18/3 and 1/3. How many times does 1/3 fit into 18/3? The answer is simply 18, as the numerators directly show the number of times the smaller fraction is contained within the larger fraction.
This method emphasizes the importance of understanding equivalent fractions and the concept of common denominators. While it might seem slightly more laborious than the reciprocal method, it provides a deeper understanding of fraction manipulation.
Understanding Equivalent Fractions
This method relies on the principle of equivalent fractions. A fraction remains the same value if both its numerator and denominator are multiplied or divided by the same number (excluding zero). This concept is vital in performing various fractional operations and solving more complex problems.
Method 3: Repeated Subtraction
A less efficient, but conceptually illuminating, approach involves repeated subtraction. We can repeatedly subtract 1/3 from 6 until we reach zero. However, since we are dealing with a fraction and a whole number, it's more practical to convert 6 into thirds. We know that 6 is equivalent to 18/3. Then we repeatedly subtract 1/3 from 18/3:
18/3 - 1/3 = 17/3 17/3 - 1/3 = 16/3 ...and so on until we reach 0/3.
Counting the number of subtractions, we arrive at the answer: 18.
This method, while more time-consuming for larger numbers, clearly demonstrates the meaning of division as repeated subtraction. It reinforces the concept of how many times a smaller value fits into a larger value.
Extending the Concept: Applications and Further Exploration
The seemingly simple problem of "How many 1/3s are in 6?" extends far beyond a basic arithmetic exercise. The underlying principles and methods of solution have broad applications in various fields:
-
Cooking and Baking: Recipes often require fractional measurements. Understanding fraction division is essential for scaling recipes up or down. If a recipe calls for 1/3 cup of sugar and you want to triple the recipe, you'll need to know how many 1/3 cups are in 3 (which is 9).
-
Construction and Engineering: Precise measurements are critical. Calculations involving fractions are common when dealing with materials and dimensions. Understanding fraction division ensures accuracy in design and construction.
-
Finance and Economics: Fractional values are ubiquitous in finance, from stock prices to interest rates. The ability to perform calculations involving fractions is essential for financial literacy and investment decision-making.
-
Data Analysis and Statistics: Fractions are frequently used in statistical calculations and data representation. A solid understanding of fraction manipulation is crucial for interpreting and analyzing data accurately.
Conclusion: Mastering Fractions for a Broader Mathematical Understanding
The question of "How many 1/3s are in 6?" provides a springboard for exploring the fascinating world of fractions and division. While the answer (18) might be easily obtained, the methods used to arrive at this answer highlight fundamental mathematical principles with wide-ranging applications. By understanding these methods—reciprocal multiplication, converting to a common denominator, and repeated subtraction—we gain a deeper appreciation for the interconnectedness of mathematical concepts and their relevance in various real-world contexts. Mastering these concepts builds a strong foundation for tackling more complex mathematical problems and enhances problem-solving skills in various fields. So, next time you encounter a seemingly simple question involving fractions, remember the depth of understanding it can unlock.
Latest Posts
Related Post
Thank you for visiting our website which covers about How Many 1/3 Are In 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.