How Many 1/2 To Make 3/4
listenit
May 10, 2025 · 5 min read
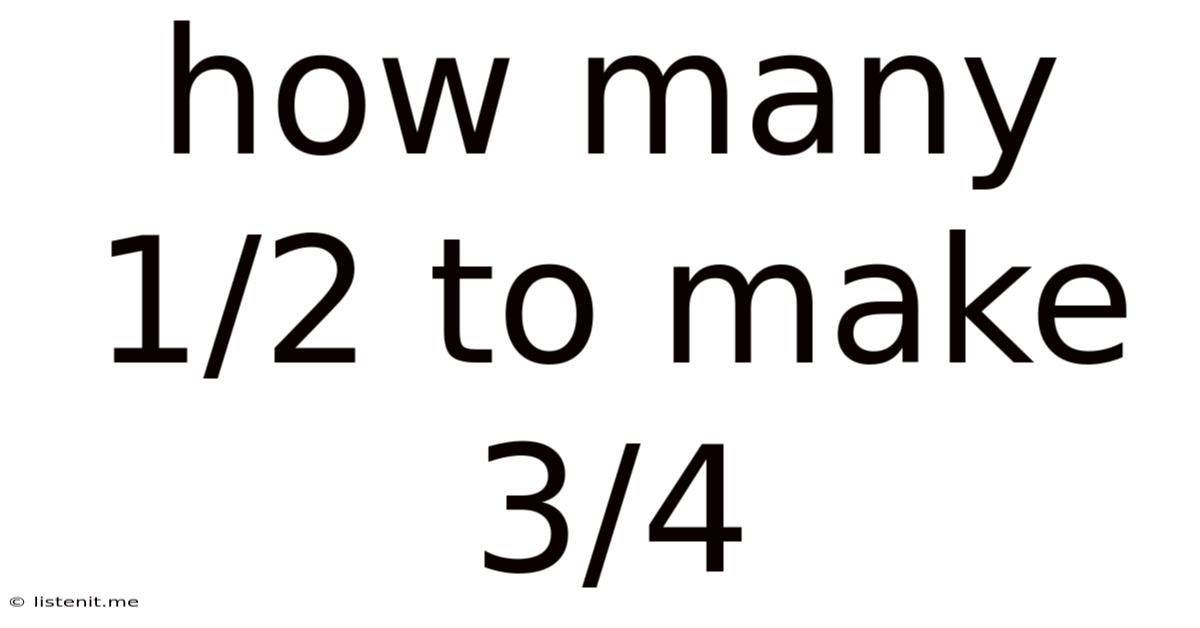
Table of Contents
How Many 1/2s Make 3/4? A Deep Dive into Fractions
Understanding fractions is a fundamental skill in mathematics, crucial for various aspects of life, from cooking and construction to advanced scientific calculations. This seemingly simple question – "How many 1/2s make 3/4?" – provides an excellent opportunity to delve into the world of fractions and explore different approaches to solving such problems. We'll not only answer the question but also explore the underlying concepts, providing you with a solid foundation for tackling more complex fractional problems.
Understanding Fractions: A Quick Refresher
Before we dive into the core problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator is 1 and the denominator is 2. This means we have one out of two equal parts of a whole. Similarly, 3/4 means we have three out of four equal parts.
Visualizing the Problem: The Power of Representation
One of the most effective ways to understand fractions is to visualize them. Imagine a pizza cut into four equal slices. 3/4 of the pizza represents three of those four slices. Now, imagine another pizza cut into two equal halves. The question "How many 1/2s make 3/4?" essentially asks: how many of these half-pizzas (1/2) are needed to equal the amount represented by three-quarters (3/4) of the first pizza?
Method 1: Using Equivalent Fractions
This is a common and efficient method for solving problems involving fractions. The key is to find a common denominator for both fractions, allowing for direct comparison and calculation.
-
Find a common denominator: The denominators of our fractions are 2 and 4. The least common multiple (LCM) of 2 and 4 is 4. This will be our common denominator.
-
Convert to equivalent fractions: We need to convert 1/2 to an equivalent fraction with a denominator of 4. To do this, we multiply both the numerator and the denominator by 2: (1 x 2) / (2 x 2) = 2/4. This means 1/2 is equivalent to 2/4.
-
Compare the fractions: Now we can compare 2/4 (representing 1/2) to 3/4. We can clearly see that we need 1 ½ of 2/4 (or 1/2) to equal 3/4. To be precise we need one full 1/2 and one half of another 1/2. This means 1.5 of 1/2 makes 3/4
Method 2: Division of Fractions
This method utilizes the concept of dividing one fraction by another. It provides a more algebraic approach to solving the problem.
-
Set up the division: To find out how many 1/2s are in 3/4, we can set up a division problem: (3/4) ÷ (1/2).
-
Invert and multiply: Dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of 1/2 is 2/1 (or simply 2). So, the problem becomes: (3/4) x (2/1).
-
Multiply the numerators and denominators: Multiply the numerators together (3 x 2 = 6) and the denominators together (4 x 1 = 4). This gives us the fraction 6/4.
-
Simplify the fraction: The fraction 6/4 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 2. This results in 3/2.
-
Interpret the result: The result 3/2 means that there are 1 ½ halves in three-quarters.
Method 3: Using a Number Line
A visual representation on a number line can be particularly helpful for understanding this concept.
-
Draw a number line: Create a number line marked with increments of 1/4.
-
Locate 3/4: Mark the point representing 3/4 on the number line.
-
Locate 1/2: Mark the point representing 1/2 on the number line.
-
Count the 1/2s: Observe how many 1/2s fit into the distance from 0 to 3/4. You’ll visually see that it takes one and a half (1 ½) of the 1/2 increments to reach 3/4.
Practical Applications: Real-World Examples
Understanding fractions isn't just an academic exercise. It's a skill with numerous practical applications in everyday life. Here are a few examples:
-
Cooking: Recipes often require fractional measurements. Knowing how to manipulate fractions ensures accurate ingredient proportions. For instance, a recipe might call for 3/4 cup of sugar, and you might need to determine how many 1/2 cup measurements to use.
-
Construction and Engineering: Precision is paramount in construction and engineering projects. Fractions are used extensively in measurements and calculations, ensuring that structures are built to the correct specifications.
-
Finance: Understanding fractions is crucial for managing personal finances. Calculating percentages, interest rates, and portions of investments often involves fractional calculations.
-
Data Analysis: Many fields rely on data analysis, and interpreting data frequently involves working with fractions and proportions.
Expanding on the Concept: More Complex Fraction Problems
The principles discussed here can be applied to more complex problems involving fractions. For example, you could ask:
- How many 1/3s make 2/5?
- How many 2/3s make 5/6?
- How many 3/8s make 1 1/2?
Solving these problems involves the same core concepts: finding common denominators, converting to equivalent fractions, or using division of fractions. With practice, you'll become adept at tackling increasingly complex fractional calculations.
Conclusion: Mastering Fractions for Success
Understanding how many 1/2s make 3/4, and more broadly, mastering the manipulation of fractions, is a vital skill with far-reaching applications. Whether you're baking a cake, building a house, or analyzing data, a strong grasp of fractions will enhance your ability to solve problems accurately and efficiently. The methods outlined above—using equivalent fractions, dividing fractions, and visual representations—provide multiple pathways to success, allowing you to choose the approach that best suits your learning style and the complexity of the problem. Consistent practice and the application of these methods will solidify your understanding and build confidence in tackling any fractional challenge. Remember that the key is to break down complex problems into smaller, manageable steps, and the solution will become clear.
Latest Posts
Latest Posts
-
The Roman Numeral In The Chemical Name Represents The
May 10, 2025
-
Liquid Changing To Gas Is Called
May 10, 2025
-
What Property Of Water Makes It The Universal Solvent
May 10, 2025
-
What Are Standard Conditions For Gas Measurements
May 10, 2025
-
Classify The Following Molecule As Chiral Or Achiral
May 10, 2025
Related Post
Thank you for visiting our website which covers about How Many 1/2 To Make 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.