How Many 1 2 Cups Make 2 3 Cup
listenit
May 12, 2025 · 4 min read
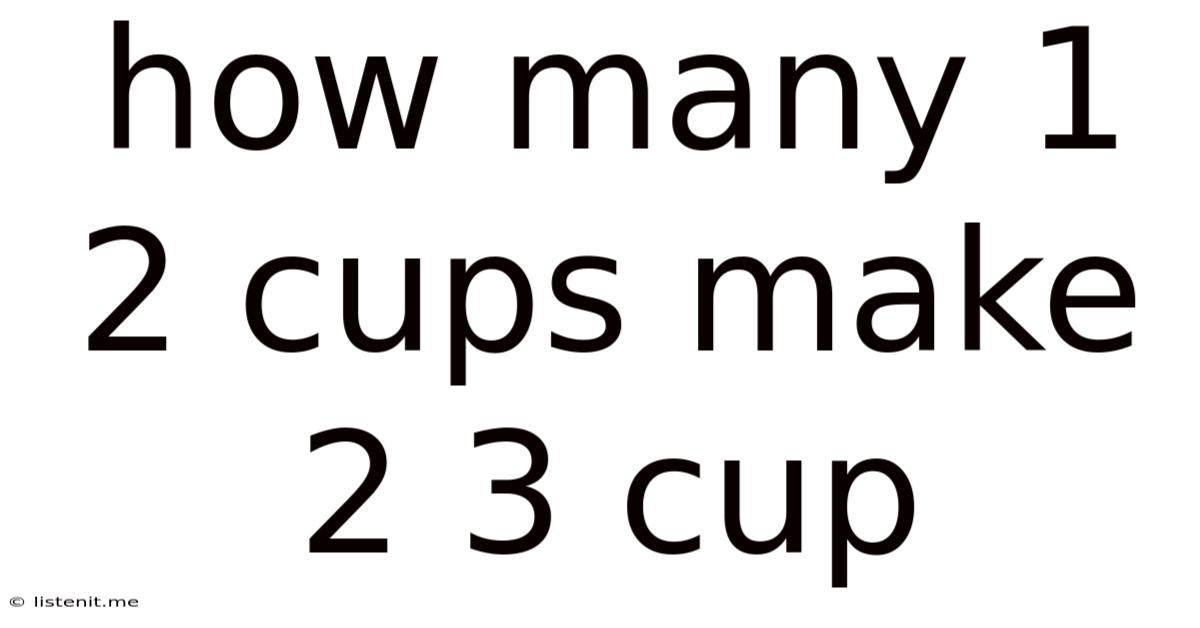
Table of Contents
How Many 1/2 Cups Make 2/3 Cup? A Deep Dive into Fraction Conversions
This seemingly simple question – "How many 1/2 cups make 2/3 cup?" – actually opens the door to a fascinating exploration of fractions, conversions, and practical applications in everyday life, particularly in cooking and baking. While a quick calculation might suffice, understanding the underlying principles will empower you to confidently tackle similar fraction problems in any context. This article will not only answer the question directly but also delve into the methods, explain the reasoning, and offer practical examples to solidify your understanding.
Understanding the Core Concept: Fractions and Equivalents
Before we jump into the calculation, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts make up the whole.
In our problem, we're dealing with 1/2 and 2/3. 1/2 represents one out of two equal parts, while 2/3 represents two out of three equal parts. The key to solving this is finding a common denominator, a number that both 2 and 3 can divide into evenly. This allows us to compare and combine fractions accurately.
Method 1: Finding the Common Denominator
The most straightforward method is to find the least common multiple (LCM) of the denominators, 2 and 3. The LCM of 2 and 3 is 6. We will convert both fractions to have a denominator of 6:
-
Converting 1/2: To change the denominator from 2 to 6, we multiply both the numerator and denominator by 3: (1 x 3) / (2 x 3) = 3/6
-
Converting 2/3: To change the denominator from 3 to 6, we multiply both the numerator and denominator by 2: (2 x 2) / (3 x 2) = 4/6
Now we have the equivalent fractions: 1/2 = 3/6 and 2/3 = 4/6.
Method 2: Using Decimal Equivalents
Alternatively, we can convert the fractions to their decimal equivalents. This method is particularly useful when dealing with more complex fractions or when using a calculator:
-
1/2: 1 divided by 2 = 0.5
-
2/3: 2 divided by 3 ≈ 0.6667 (this is a repeating decimal)
To find out how many 0.5 cups are in approximately 0.6667 cups, we divide 0.6667 by 0.5: 0.6667 / 0.5 ≈ 1.333
This tells us that approximately 1.333 half cups make 2/3 cup.
Solving the Problem: The Answer and Its Interpretation
Using either method, we arrive at a similar answer. While Method 1 (using the common denominator) provides a more precise answer in fraction form (4/6 divided by 3/6 = 4/3), Method 2 provides a more practical decimal approximation. Let's analyze both:
-
Fraction Method: We found that 2/3 cup is equal to 4/6 cup, and 1/2 cup is equal to 3/6 cup. Therefore, to find how many 1/2 cups (3/6) are in 2/3 cups (4/6), we divide 4/6 by 3/6 which simplifies to 4/3. This means it takes 1 and 1/3 half cups to make 2/3 of a cup.
-
Decimal Method: The decimal approximation of 1.333 confirms the fraction method. We need slightly more than one half-cup, specifically about one and a third.
Practical Applications: Cooking, Baking, and Beyond
Understanding fraction conversions is crucial in many aspects of life. Consider these examples:
-
Baking: A recipe might call for 2/3 cup of flour, but your measuring cups only have 1/2 cup increments. Knowing how to convert allows you to accurately measure the ingredient.
-
Cooking: Scaling recipes up or down requires accurate fraction conversions. If you want to halve a recipe that calls for 2/3 cup of sugar, you'll need to know how much that is in 1/2 cup measurements.
-
Construction and Engineering: Precise measurements are essential, and fractions often play a key role in calculations.
-
Everyday Life: Dividing tasks, sharing resources, or understanding proportions all involve fractions.
Extending Your Knowledge: Working with More Complex Fractions
The principles discussed here can be applied to more complex fraction conversions. Remember these key steps:
- Find a common denominator: This is the foundation of adding, subtracting, and comparing fractions.
- Simplify the fractions: Reduce fractions to their simplest forms to make calculations easier.
- Use decimal equivalents (when appropriate): Decimal equivalents are helpful for practical applications and when using calculators.
- Practice: The more you practice solving fraction problems, the more comfortable and confident you'll become.
Conclusion: Mastering Fraction Conversions for a More Accurate Life
Understanding how many 1/2 cups make 2/3 cup is more than just solving a simple math problem; it's about grasping a fundamental concept with wide-ranging practical applications. By mastering fraction conversions, you equip yourself with a valuable skill that enhances accuracy in various areas of life, from cooking and baking to more complex fields like engineering and science. The ability to confidently manipulate fractions translates to precise measurements, better recipe scaling, and ultimately, a greater understanding of the world around us. So, remember the methods outlined here, practice regularly, and enjoy the empowerment that comes with a solid grasp of fractions!
Latest Posts
Latest Posts
-
What Is The Greatest Common Factor Of 30 And 18
May 13, 2025
-
How To Find Area Of A Triangle With Points
May 13, 2025
-
What Is The Reciprocal Of 6 5
May 13, 2025
-
What Is The Analogy Of Nucleus
May 13, 2025
-
Is Ionization Energy Endothermic Or Exothermic
May 13, 2025
Related Post
Thank you for visiting our website which covers about How Many 1 2 Cups Make 2 3 Cup . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.