How Many 1/2 Are In 7
listenit
May 25, 2025 · 5 min read
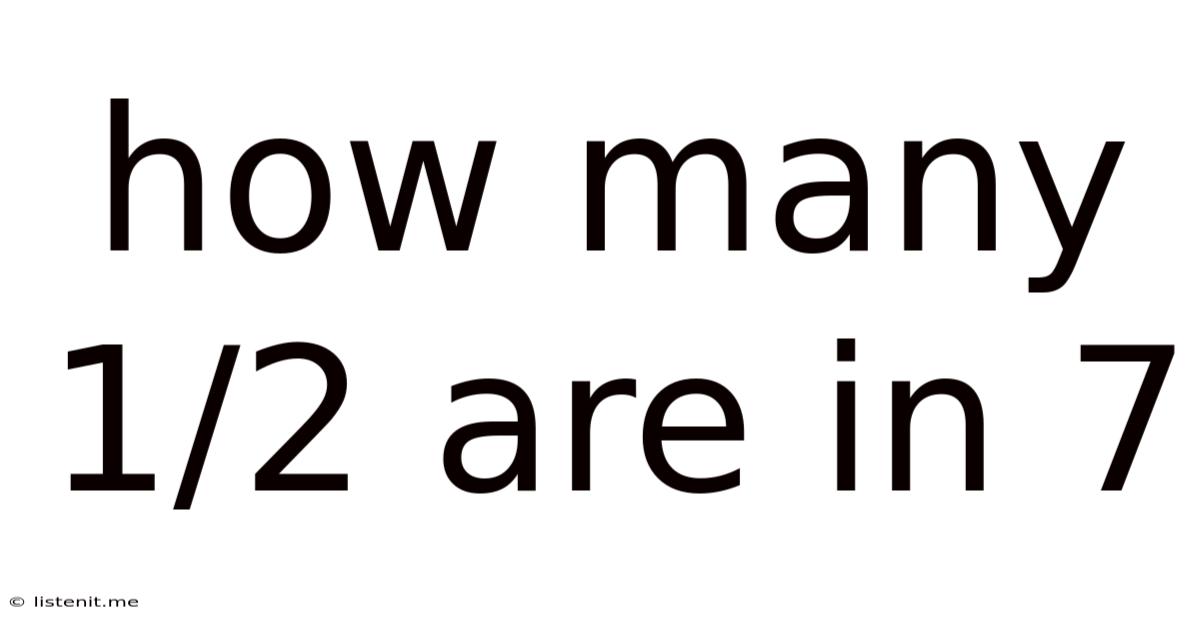
Table of Contents
How Many Halves Are in 7? A Deep Dive into Fractions and Division
This seemingly simple question, "How many 1/2 are in 7?", opens the door to a fascinating exploration of fractions, division, and their practical applications. While the immediate answer might seem obvious, a deeper understanding reveals crucial mathematical concepts and problem-solving strategies applicable far beyond this specific query. This article will not only provide the solution but will also delve into the underlying principles, offering multiple approaches and exploring related concepts to solidify your understanding.
Understanding the Problem: Fractions and Division
At its core, this question asks us to divide 7 by 1/2. This is a fundamental division problem involving fractions. Many find fraction division challenging, but with a clear understanding of the process, it becomes straightforward. Remember that division essentially asks, "How many times does one number fit into another?" In this case, we want to know how many times 1/2 fits into 7.
Visualizing the Problem
One effective way to visualize this problem is to imagine you have seven whole pies. Each pie can be cut into two halves (1/2). How many halves do you have in total? This visual representation immediately suggests a multiplication approach: 7 pies x 2 halves/pie = 14 halves.
Method 1: Direct Division of Fractions
The most direct approach to solving this problem involves the standard method of dividing fractions. Remember the rule: to divide by a fraction, multiply by its reciprocal.
The reciprocal of 1/2 is 2/1 (or simply 2). Therefore, the problem becomes:
7 ÷ 1/2 = 7 x 2/1 = 7 x 2 = 14
Therefore, there are 14 halves in 7.
Applying this Method to other Scenarios
This method isn't limited to whole numbers divided by 1/2. Let's consider a slightly more complex example: How many 2/3 are in 5?
- Find the reciprocal of 2/3: The reciprocal is 3/2.
- Multiply: 5 x 3/2 = 15/2 = 7.5
This means there are 7.5 instances of 2/3 in 5.
Method 2: Converting to a Common Denominator
Another approach involves converting the whole number into a fraction with the same denominator as the fraction we're dividing by. Since we're dealing with halves, we can convert 7 into a fraction with a denominator of 2:
7 = 14/2
Now, the problem becomes:
14/2 ÷ 1/2
When dividing fractions with the same denominator, we simply divide the numerators:
14 ÷ 1 = 14
Again, we arrive at the answer: there are 14 halves in 7.
Extending this Method
This method, like the previous one, is adaptable to various fraction division problems. For example, to find how many 3/4 are in 6, we would first convert 6 to a fraction with a denominator of 4: 6 = 24/4. Then we divide: 24/4 ÷ 3/4 = 24/3 = 8. Therefore, there are 8 instances of 3/4 in 6.
Method 3: Using a Real-World Analogy
Stepping away from pure mathematical manipulation, we can use a real-world analogy to illustrate the concept. Imagine you are baking cookies. A recipe calls for 1/2 cup of sugar for one batch of cookies. If you have 7 cups of sugar, how many batches of cookies can you make?
This directly translates to the original problem: 7 ÷ 1/2. The solution, as we've established, is 14 batches.
Practical Applications of Fraction Division
Understanding fraction division isn't just about solving mathematical problems; it has significant practical applications across various fields:
- Cooking and Baking: Adjusting recipes, calculating ingredient quantities, and understanding portion sizes often require dividing fractions.
- Construction and Engineering: Precision measurements and calculations necessitate a strong grasp of fraction division.
- Sewing and Tailoring: Cutting fabric accurately, adjusting patterns, and understanding fabric requirements often involve fraction calculations.
- Finance: Calculating interest rates, shares of ownership, and proportions of investments all require proficiency in working with fractions.
Beyond the Basics: Exploring Related Concepts
This problem provides a springboard to explore several interconnected mathematical concepts:
Reciprocal Numbers
The concept of reciprocals plays a crucial role in fraction division. Understanding reciprocals helps simplify and streamline the division process, making it more manageable. Remember that the reciprocal of a fraction is formed by simply switching the numerator and the denominator.
Equivalent Fractions
Recognizing and working with equivalent fractions is essential for simplifying calculations and solving problems efficiently. Converting fractions to a common denominator, as demonstrated in Method 2, simplifies the division process.
Decimal Representation of Fractions
It's often helpful to convert fractions into their decimal equivalents. In this case, 1/2 is equivalent to 0.5. The problem then becomes 7 ÷ 0.5 = 14. This approach can be particularly useful when dealing with more complex fractions or when using calculators.
Troubleshooting Common Mistakes
When working with fraction division, several common mistakes can lead to incorrect answers:
- Forgetting the reciprocal: A frequent error is failing to multiply by the reciprocal of the divisor.
- Incorrectly multiplying or dividing numerators and denominators: Care must be taken to correctly perform the multiplication or division of the numerators and denominators.
- Improper simplification of fractions: Simplifying fractions after the division is crucial to obtain the most concise and accurate answer.
Conclusion: Mastering Fraction Division
The seemingly simple question "How many 1/2 are in 7?" provides a valuable opportunity to explore the fundamentals of fraction division. By understanding the various methods – direct division, converting to a common denominator, and using real-world analogies – you develop a solid foundation for tackling more complex fraction problems. Remember the importance of reciprocals, equivalent fractions, and the possibility of using decimal representation. By mastering these concepts and avoiding common pitfalls, you enhance your mathematical abilities and develop skills applicable to various practical situations. The solution, 14, represents not just an answer but a gateway to a deeper understanding of mathematical principles. Continue practicing and exploring to solidify your understanding and conquer the world of fractions!
Latest Posts
Latest Posts
-
How To Work Out Golf Handicap
May 25, 2025
-
How Many Days Are 5 Years
May 25, 2025
-
What Is 0 5 As A Percentage
May 25, 2025
-
What Is The Gcf Of 32 And 18
May 25, 2025
-
How Many Years Ago Was 1976
May 25, 2025
Related Post
Thank you for visiting our website which covers about How Many 1/2 Are In 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.