Highest Common Factor Of 28 And 42
listenit
Apr 05, 2025 · 5 min read
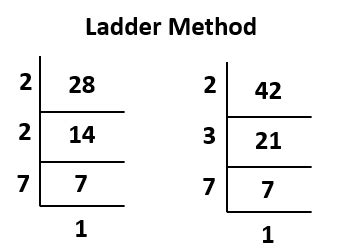
Table of Contents
Finding the Highest Common Factor (HCF) of 28 and 42: A Comprehensive Guide
The highest common factor (HCF), also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. Finding the HCF is a fundamental concept in number theory with applications in various fields, from simplifying fractions to solving complex mathematical problems. This article will delve deep into determining the HCF of 28 and 42, exploring multiple methods and providing a comprehensive understanding of the underlying principles.
Understanding Factors and Common Factors
Before we dive into calculating the HCF of 28 and 42, let's solidify our understanding of factors and common factors.
Factors are numbers that divide exactly into a given number without leaving a remainder. For instance, the factors of 28 are 1, 2, 4, 7, 14, and 28. Similarly, the factors of 42 are 1, 2, 3, 6, 7, 14, 21, and 42.
Common factors are numbers that are factors of two or more numbers. Looking at the factors of 28 and 42, we can see that some numbers appear in both lists: 1, 2, 7, and 14. These are the common factors of 28 and 42.
The highest common factor (HCF) is simply the largest of these common factors. In our example, the HCF of 28 and 42 is 14.
Methods for Finding the HCF
Several methods can be used to find the HCF of two numbers. Let's explore three common and effective techniques:
1. Listing Factors Method
This is the most straightforward method, particularly suitable for smaller numbers. It involves listing all the factors of each number and then identifying the largest common factor.
- Factors of 28: 1, 2, 4, 7, 14, 28
- Factors of 42: 1, 2, 3, 6, 7, 14, 21, 42
By comparing the two lists, we can see that the common factors are 1, 2, 7, and 14. The largest of these is 14, therefore, the HCF of 28 and 42 is 14.
This method is simple to understand but becomes less efficient when dealing with larger numbers where listing all factors can be time-consuming.
2. Prime Factorization Method
This method involves breaking down each number into its prime factors. The prime factors are then used to determine the HCF.
- Prime factorization of 28: 2 x 2 x 7 = 2² x 7
- Prime factorization of 42: 2 x 3 x 7
Now, identify the common prime factors and their lowest powers. Both 28 and 42 share a '2' and a '7'. The lowest power of 2 is 2¹ (or simply 2), and the lowest power of 7 is 7¹.
Multiply these common prime factors together: 2 x 7 = 14. Therefore, the HCF of 28 and 42 is 14.
This method is more efficient than listing factors, especially when dealing with larger numbers.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the HCF, especially for larger numbers. It's based on the principle that the HCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the HCF.
Let's apply the Euclidean algorithm to find the HCF of 28 and 42:
- Divide the larger number (42) by the smaller number (28): 42 ÷ 28 = 1 with a remainder of 14.
- Replace the larger number (42) with the remainder (14): Now we find the HCF of 28 and 14.
- Divide the larger number (28) by the smaller number (14): 28 ÷ 14 = 2 with a remainder of 0.
- Since the remainder is 0, the HCF is the last non-zero remainder, which is 14.
Therefore, the HCF of 28 and 42 is 14.
The Euclidean algorithm is particularly efficient for large numbers because it avoids the need to find all factors.
Applications of HCF
The HCF has numerous applications across various mathematical and real-world scenarios:
-
Simplifying Fractions: The HCF is used to simplify fractions to their lowest terms. For example, the fraction 42/28 can be simplified by dividing both the numerator and denominator by their HCF (14), resulting in the simplified fraction 3/2.
-
Solving Word Problems: Many word problems involving division and sharing require finding the HCF to determine the largest possible equal groups or quantities.
-
Geometry: HCF plays a role in solving geometrical problems related to finding the dimensions of shapes or dividing areas into equal parts.
-
Number Theory: The HCF is a fundamental concept in number theory, used in more advanced topics like modular arithmetic and cryptography.
-
Computer Science: Algorithms related to finding the HCF are used in various computer science applications, including cryptography and data compression.
Beyond Two Numbers: Extending the HCF Concept
While we've focused on finding the HCF of two numbers, the concept can be extended to find the HCF of three or more numbers. The same methods, particularly the prime factorization and Euclidean algorithm methods, can be adapted to handle multiple numbers.
For example, to find the HCF of 28, 42, and 56:
-
Prime Factorization:
- 28 = 2² x 7
- 42 = 2 x 3 x 7
- 56 = 2³ x 7
The common prime factors are 2 and 7. The lowest power of 2 is 2¹, and the lowest power of 7 is 7¹. Therefore, the HCF of 28, 42, and 56 is 2 x 7 = 14.
-
Euclidean Algorithm (for multiple numbers): The Euclidean algorithm can be extended by finding the HCF of two numbers at a time, iteratively. First, find the HCF of two numbers (e.g., 28 and 42), and then find the HCF of the result and the third number (e.g., HCF(14, 56)).
Conclusion
Finding the highest common factor (HCF) is a fundamental skill in mathematics with diverse applications. This article has explored various methods – listing factors, prime factorization, and the Euclidean algorithm – providing a thorough understanding of how to determine the HCF, particularly focusing on the example of 28 and 42. The chosen method depends on the context and the size of the numbers involved. For smaller numbers, listing factors is adequate, while the prime factorization and Euclidean algorithm methods are more efficient for larger numbers. The understanding of HCF is not just limited to two numbers and can be extended to multiple numbers using the same fundamental principles. Mastering these methods will equip you with a valuable tool for solving a wide range of mathematical problems.
Latest Posts
Related Post
Thank you for visiting our website which covers about Highest Common Factor Of 28 And 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
