Graph Y 3 1 2 X 2
listenit
May 13, 2025 · 5 min read
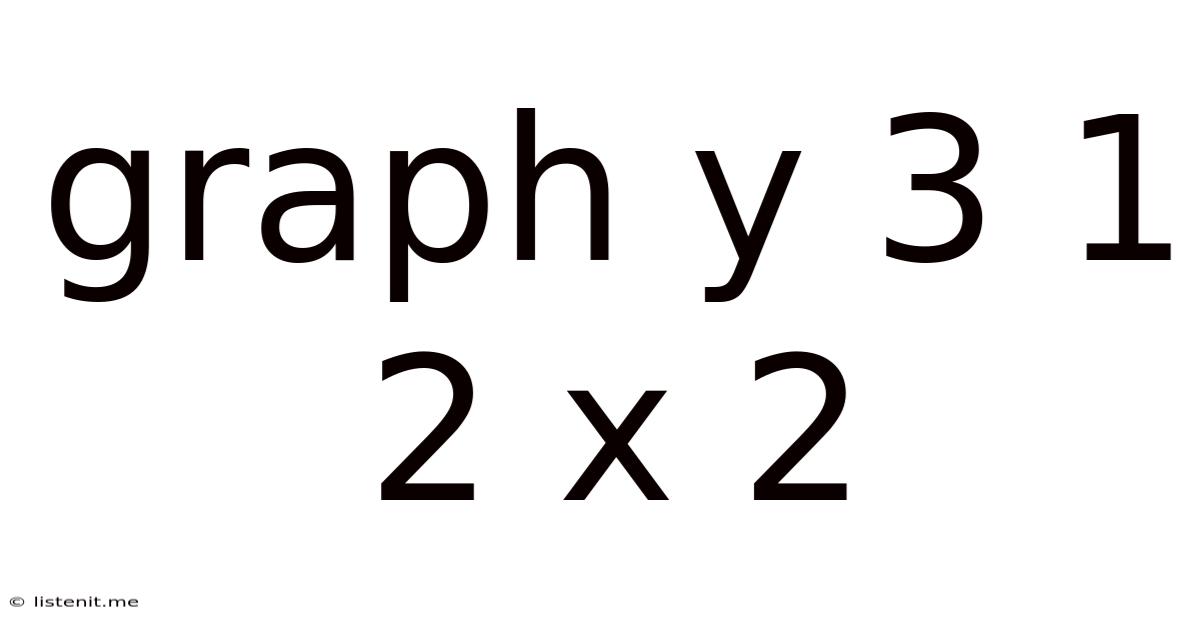
Table of Contents
Decoding the Graph: A Comprehensive Exploration of y = 3/(1 + 2x²)
The equation y = 3/(1 + 2x²) presents a fascinating challenge for mathematical exploration. This seemingly simple equation reveals a rich tapestry of mathematical concepts, ranging from basic function analysis to more advanced calculus techniques. This article will delve into a comprehensive analysis of this graph, exploring its key features, characteristics, and the underlying mathematical principles that govern its behavior. We'll journey from understanding its basic shape to analyzing its derivatives, asymptotes, and other crucial properties.
Understanding the Basic Function
At its core, y = 3/(1 + 2x²) represents a rational function. Rational functions are defined as the ratio of two polynomial functions. In this case, the numerator is a constant polynomial (3) and the denominator is a quadratic polynomial (1 + 2x²). This specific structure dictates several key features of the graph.
Key Features:
-
Even Function: The function is an even function because f(-x) = f(x). This means that the graph is symmetric about the y-axis. Replacing 'x' with '-x' leaves the equation unchanged, confirming its even nature. This symmetry simplifies our analysis considerably.
-
Positive Values: The numerator is always positive (3), and the denominator (1 + 2x²) is always positive since x² is always non-negative. Therefore, y is always positive for all real values of x. This means the graph lies entirely above the x-axis.
-
Horizontal Asymptote: As x approaches positive or negative infinity (x → ±∞), the denominator (1 + 2x²) becomes significantly larger than the numerator (3). Consequently, the value of y approaches zero (y → 0). This indicates the presence of a horizontal asymptote at y = 0. The graph gets arbitrarily close to the x-axis but never actually touches it.
-
Maximum Value: The function achieves its maximum value when the denominator is minimized. Since 1 + 2x² is always greater than or equal to 1 (minimum value occurs at x = 0), the maximum value of y is 3, which occurs at x = 0. This point (0, 3) represents the highest point on the graph.
Analyzing the Graph's Shape
The graph's shape is best described as a bell curve, or more accurately, a bell-shaped curve that is symmetrical around the y-axis. It starts at its maximum point (0, 3) and gradually decreases as x moves away from zero in either the positive or negative direction. The curve approaches the x-axis asymptotically, never quite reaching it.
Visual Representation:
Although we can't physically display the graph here, imagine a smooth, bell-shaped curve that peaks at (0, 3) and descends symmetrically towards the x-axis as x extends to infinity in both positive and negative directions. The x-axis acts as a horizontal asymptote, guiding the curve's approach towards zero without ever actually touching it.
Calculus Approach: Derivatives and Concavity
To further deepen our understanding, let's analyze the function using calculus.
First Derivative:
The first derivative, dy/dx, provides information about the slope of the tangent line at any point on the curve. It helps us identify increasing and decreasing intervals.
Applying the quotient rule, we get:
dy/dx = -12x / (1 + 2x²)²
The first derivative is zero at x = 0. For x > 0, the derivative is negative, indicating a decreasing function. For x < 0, the derivative is positive, indicating an increasing function. This confirms our observation that the function increases up to x = 0 and then decreases.
Second Derivative:
The second derivative, d²y/dx², gives us insights into the concavity of the function.
d²y/dx² = (12(4x² - 1)) / (1 + 2x²)³
Setting the second derivative to zero:
12(4x² - 1) = 0
This gives us x = ±1/2.
Analyzing the intervals:
- x < -1/2: d²y/dx² > 0 (concave up)
- -1/2 < x < 1/2: d²y/dx² < 0 (concave down)
- x > 1/2: d²y/dx² > 0 (concave up)
This reveals that the function is concave up for x < -1/2 and x > 1/2, and concave down for -1/2 < x < 1/2. The points x = ±1/2 are inflection points, where the concavity changes.
Asymptotes and Domain/Range
We've already established the horizontal asymptote at y = 0. This function doesn't have any vertical asymptotes because the denominator (1 + 2x²) is never equal to zero for any real value of x.
Domain and Range:
-
Domain: The domain of the function is all real numbers (-∞, ∞). There are no restrictions on the values of x.
-
Range: The range is (0, 3]. The function's values are always positive, approaching zero as x approaches infinity and reaching a maximum value of 3 at x = 0.
Applications and Further Exploration
This seemingly simple function has practical applications in various fields, though these applications might not be immediately apparent from the equation alone. Its shape and characteristics make it useful in modeling certain phenomena that exhibit a bell-shaped distribution, such as probability distributions or certain types of physical processes.
Further Exploration:
-
Transformations: Explore how altering the constants in the equation (e.g., changing the '3' in the numerator or the '2' in the denominator) affects the graph's shape, maximum value, and asymptotes.
-
Integration: Investigate the integral of the function. This can be challenging but offers a deeper understanding of the area under the curve.
-
Numerical Methods: Explore how numerical methods, like Newton-Raphson, can be used to find approximate solutions to equations involving this function.
-
Three-Dimensional Extensions: Consider extending the concept to three dimensions by exploring related surface equations.
Conclusion:
The equation y = 3/(1 + 2x²) offers a rich platform for exploring fundamental concepts in mathematics. Through analysis of its features, derivatives, asymptotes, and domain/range, we gain a deeper appreciation for the relationship between algebraic expressions and their graphical representations. The journey of understanding this seemingly simple function opens doors to more complex mathematical concepts and their applications across various scientific and engineering disciplines. This exploration highlights the power of mathematical analysis in providing insights into the behavior and properties of functions. The symmetrical, bell-shaped curve serves as a visually intuitive example of many mathematical principles in action.
Latest Posts
Latest Posts
-
What Does It Mean To Have High Specific Heat
May 13, 2025
-
Chemical Formula For Chromium Iii Nitrate
May 13, 2025
-
Write 1 8 As A Decimal
May 13, 2025
-
Area Of Parallelogram With 4 Vertices
May 13, 2025
-
3 1 2 In Improper Fraction
May 13, 2025
Related Post
Thank you for visiting our website which covers about Graph Y 3 1 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.