Graph X 2 Y 2 9
listenit
Mar 28, 2025 · 5 min read
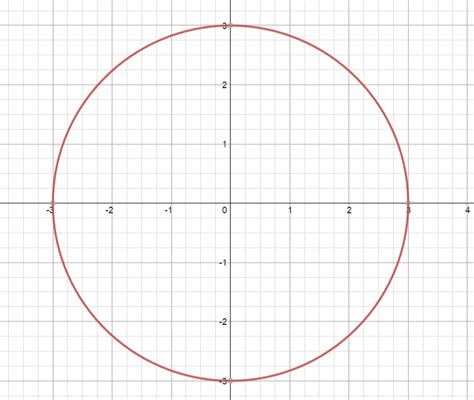
Table of Contents
Unveiling the Secrets of the Graph x² + y² = 9: A Comprehensive Exploration
The equation x² + y² = 9 might seem simple at first glance, but it represents a fundamental concept in mathematics with far-reaching applications across various fields. This article delves deep into the intricacies of this equation, exploring its graphical representation, properties, transformations, and real-world applications. We'll uncover the beauty and power hidden within this seemingly straightforward algebraic expression.
Understanding the Equation: A Circle's Identity
The equation x² + y² = 9 defines a circle in a Cartesian coordinate system. Let's break down why:
- x² and y²: These terms represent the squares of the x and y coordinates of any point on the graph.
- Summation: The '+' sign indicates that we're summing the squares of the x and y coordinates.
- Equality to 9: This constant value determines the size of the circle. It's crucial to understand that this number is the square of the radius.
Therefore, the equation essentially states that for any point (x, y) on the graph, the sum of the squares of its coordinates is always equal to 9. This directly translates to the Pythagorean theorem, a cornerstone of geometry, suggesting a relationship between the sides of a right-angled triangle.
Visualizing the Graph: A Circle with Radius 3
The graphical representation of x² + y² = 9 is a circle centered at the origin (0, 0) with a radius of 3. This is because the equation can be rewritten as:
x² + y² = 3²
This clearly shows that the radius (r) is 3. Every point on the circle is exactly 3 units away from the center. You can visualize this by plotting points: (3, 0), (-3, 0), (0, 3), (0, -3), and many more that satisfy the equation.
Key Properties of the Circle: Exploring its Characteristics
The circle defined by x² + y² = 9 possesses several key properties:
- Center: The center of the circle is located at the origin (0, 0).
- Radius: The radius of the circle is 3 units.
- Diameter: The diameter of the circle is twice the radius, which is 6 units.
- Circumference: The circumference (C) of the circle can be calculated using the formula C = 2πr, where r is the radius. In this case, C = 2π(3) = 6π units.
- Area: The area (A) of the circle can be calculated using the formula A = πr², where r is the radius. In this case, A = π(3)² = 9π square units.
- Symmetry: The circle is symmetrical about both the x-axis and the y-axis. This means that if a point (x, y) lies on the circle, then so do the points (-x, y), (x, -y), and (-x, -y).
Transformations: Shifting and Scaling the Circle
The basic equation x² + y² = 9 can be transformed to create circles with different centers and radii. Let's explore some common transformations:
-
Translation: Adding or subtracting constants from x and y shifts the circle's center. For example, (x - 2)² + (y + 1)² = 9 represents a circle with its center at (2, -1) and a radius of 3.
-
Scaling: Multiplying x and y by constants scales the circle. For example, (2x)² + (2y)² = 9 represents a circle with a radius of 3/2, centered at the origin. Note that scaling affects both the radius and the diameter.
Extending the Concepts: Beyond the Basics
The equation x² + y² = 9 is a fundamental building block for understanding more complex concepts in mathematics:
- Conic Sections: Circles belong to a family of curves called conic sections, which also include ellipses, parabolas, and hyperbolas. Understanding circles provides a strong foundation for grasping these other curves.
- Trigonometry: The unit circle (x² + y² = 1) is a critical tool in trigonometry. The equation x² + y² = 9 provides a direct scaling relationship to the unit circle and aids in understanding trigonometric functions.
- Calculus: The equation can be used to explore concepts like arc length, area, and volumes of revolution using integral calculus.
Real-World Applications: From Engineering to Design
The concept of a circle, and by extension the equation x² + y² = 9, finds applications in diverse fields:
-
Engineering: Designing circular components in machinery, calculating the stress on circular structures, and determining the path of projectiles.
-
Architecture: Creating circular arches, domes, and other architectural features.
-
Physics: Modeling circular motion, describing the path of planets (Kepler's Laws), and understanding wave propagation.
-
Computer Graphics: Generating circles for various graphics applications, animations, and game development. The equation is fundamental in creating smooth, accurate circles.
-
Mapping and Navigation: GPS systems rely on spherical coordinates, a close relative to the Cartesian circle.
-
Data Analysis: Visualizing data using circular graphs like pie charts and polar plots relies on fundamental circle principles.
Solving Problems Using the Equation
Let's tackle a few example problems to solidify our understanding:
Problem 1: Find the distance from the origin to a point (3, 0) on the circle x² + y² = 9.
Solution: The distance is simply the radius of the circle, which is 3.
Problem 2: Is the point (2, 2) inside, outside, or on the circle x² + y² = 9?
Solution: Substitute x = 2 and y = 2 into the equation: 2² + 2² = 8, which is less than 9. Therefore, the point is inside the circle.
Problem 3: Find the equation of a circle with a radius of 5 and centered at (2, -3).
Solution: The equation is (x - 2)² + (y + 3)² = 5².
Conclusion: A Journey Through Circles
The seemingly simple equation x² + y² = 9 opens up a fascinating world of mathematical concepts and practical applications. From its graphical representation as a circle to its applications across various disciplines, this equation highlights the power of mathematical models in understanding and shaping our world. By exploring its properties, transformations, and real-world applications, we gain a deeper appreciation for the elegance and utility of this fundamental mathematical concept. This exploration underscores the importance of understanding foundational equations in building a strong base for more advanced mathematical concepts and real-world problem-solving. The journey of understanding this equation is a testament to the power of mathematics to unlock the mysteries of our universe.
Latest Posts
Latest Posts
-
Is Iodine A Metal Metalloid Or Nonmetal
Mar 31, 2025
-
Ionic Compound For Calcium And Sulfur
Mar 31, 2025
-
What Is 95 In Fraction Form
Mar 31, 2025
-
What Is 16 25 As A Percent
Mar 31, 2025
-
How Many Pints Are In 1 Pound
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Graph X 2 Y 2 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
