Graph The Function Y 2 X
listenit
May 12, 2025 · 5 min read
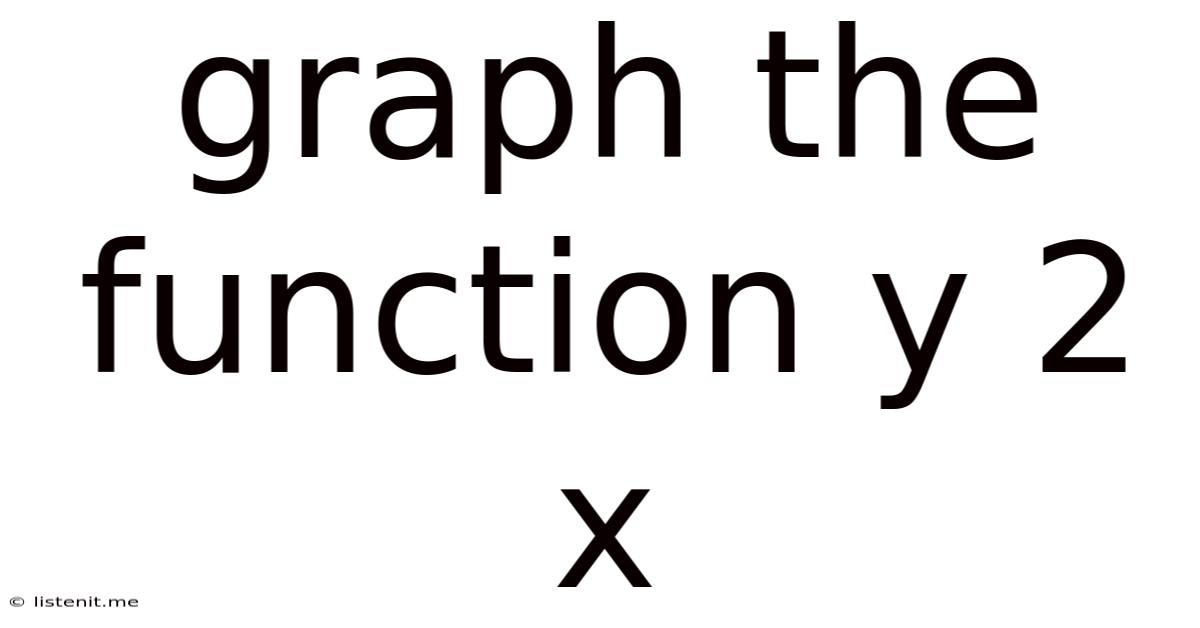
Table of Contents
Graphing the Function y = 2x: A Comprehensive Guide
The seemingly simple equation, y = 2x, represents a fundamental concept in algebra and serves as a building block for understanding more complex mathematical relationships. This article delves into a comprehensive exploration of this linear function, covering its graphical representation, characteristics, real-world applications, and extensions to related concepts.
Understanding the Equation y = 2x
At its core, y = 2x is a linear equation, meaning it represents a straight line when graphed. The equation establishes a direct relationship between the variables x and y: for every unit increase in x, y increases by two units. This constant rate of change is represented by the slope of the line. In this case, the slope is 2. The equation is in the slope-intercept form, y = mx + b, where 'm' is the slope and 'b' is the y-intercept (the point where the line crosses the y-axis). In y = 2x, the slope (m) is 2, and the y-intercept (b) is 0.
Key Characteristics of y = 2x
- Linearity: The most prominent characteristic is its linearity. This means the graph is a straight line, not a curve.
- Positive Slope: The slope of 2 is positive, indicating that as x increases, y also increases. This signifies a positive correlation between the two variables. The line ascends from left to right.
- Y-intercept at the Origin: The y-intercept is 0, meaning the line passes through the origin (0,0) of the coordinate plane.
- Constant Rate of Change: The slope of 2 represents a constant rate of change. For every one-unit change in x, y changes by two units. This consistency is a defining feature of linear functions.
- Direct Proportionality: The equation demonstrates direct proportionality. y is directly proportional to x; doubling x doubles y, tripling x triples y, and so on.
Graphing the Function
To graph y = 2x, we need to plot points that satisfy the equation and then connect them to form a straight line. Here's a step-by-step approach:
- Create a Table of Values: Choose several values for x and calculate the corresponding values for y using the equation y = 2x.
| x | y = 2x | (x, y) |
|---|---|---|
| -2 | -4 | (-2, -4) |
| -1 | -2 | (-1, -2) |
| 0 | 0 | (0, 0) |
| 1 | 2 | (1, 2) |
| 2 | 4 | (2, 4) |
-
Plot the Points: Using a Cartesian coordinate system (x-y plane), plot each (x, y) pair from the table.
-
Draw the Line: Connect the plotted points with a straight line. This line represents the graph of the function y = 2x. The line should extend beyond the plotted points to indicate that the relationship holds true for all values of x.
Important Note: Even though we only plotted five points, infinitely many points lie on the line y = 2x. Any point that satisfies the equation will be on the line.
Interpreting the Graph
The graph of y = 2x provides a visual representation of the relationship between x and y. We can use the graph to:
-
Determine the value of y for a given x: For any value of x, we can find the corresponding y-value by locating the x-value on the horizontal axis, moving vertically to the line, and then horizontally to the y-axis to read the y-value.
-
Determine the value of x for a given y: We can perform the reverse process to find the x-value corresponding to a given y-value.
-
Observe the slope: The steepness of the line visually represents the slope. A steeper line indicates a larger slope.
-
Identify intercepts: The points where the line intersects the x and y axes represent the x and y intercepts, respectively. In this case, both intercepts are at the origin (0, 0).
Real-world Applications
The function y = 2x, while seemingly simple, finds applications in various real-world scenarios:
-
Direct Proportions: Any situation involving a direct proportion between two variables can be modeled using this function. For example, the cost of buying apples (y) at $2 per apple (x) is represented by y = 2x.
-
Speed and Distance: If an object moves at a constant speed of 2 units per time unit, the distance covered (y) after a certain time (x) is given by y = 2x.
-
Scaling and Ratio: The function can model scaling situations where one quantity is consistently twice the other. For example, if you are enlarging a picture and the width of the enlarged image (y) is always twice the original width (x), then y = 2x.
-
Conversion Factors: Many unit conversions involve a simple multiplicative factor. For example, converting kilograms to pounds (with a simplified conversion) could be approximated using a linear function similar to y = 2x.
Extensions and Related Concepts
The understanding of y = 2x provides a foundation for grasping more complex mathematical concepts:
-
Linear Equations with Non-Zero Y-intercepts: The equation y = mx + b, where b ≠ 0, represents lines that do not pass through the origin. Understanding y = 2x helps to build an intuition for these more general linear equations.
-
Systems of Linear Equations: Solving systems of linear equations often involves graphing lines and finding their intersection point. Understanding the graphing of y = 2x is crucial for solving these systems.
-
Linear Inequalities: The inequality y > 2x or y < 2x represents regions of the coordinate plane above or below the line y = 2x, respectively.
-
Functions and their Graphs: y = 2x serves as a perfect example of a function, where each input (x) has exactly one output (y). Understanding this function helps to grasp the broader concept of functions and their graphical representation.
-
Slope and its Interpretations: The slope of the line, 2 in this case, plays a pivotal role in understanding rate of change, gradients, and other applications in calculus and physics.
Conclusion
The function y = 2x, while seemingly basic, is a fundamental concept in mathematics with wide-ranging applications. Through its graphical representation, we can visualize and understand the direct proportional relationship between two variables. This understanding serves as a cornerstone for more advanced mathematical concepts and real-world problem-solving. The principles and methods detailed here can be readily applied to other linear functions, providing a solid framework for tackling more intricate algebraic problems and data analysis. Mastering the understanding and graphing of such functions is crucial for success in algebra and related fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about Graph The Function Y 2 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.