Graph Of Y 4x X 2
listenit
Apr 05, 2025 · 5 min read
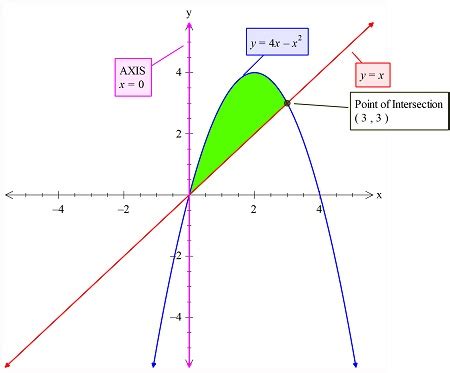
Table of Contents
Exploring the Graph of y = 4x - x²: A Comprehensive Analysis
The equation y = 4x - x² represents a parabola, a fundamental concept in algebra and calculus. Understanding its graph involves analyzing key features like its vertex, intercepts, axis of symmetry, and concavity. This comprehensive guide will delve into each of these aspects, providing a detailed exploration of this quadratic function and its visual representation. We will also explore practical applications and extensions of understanding this specific parabola.
Understanding the Quadratic Function
The equation y = 4x - x² is a quadratic function, meaning it's a polynomial of degree two. The general form of a quadratic function is y = ax² + bx + c, where 'a', 'b', and 'c' are constants. In our case, a = -1, b = 4, and c = 0. The negative value of 'a' indicates that the parabola opens downwards, meaning it has a maximum point rather than a minimum.
Identifying Key Features
Several key features help us accurately sketch and understand the graph of y = 4x - x²:
-
Vertex: The vertex represents the maximum or minimum point of the parabola. For a quadratic function in the form y = ax² + bx + c, the x-coordinate of the vertex is given by x = -b/(2a). In our case, x = -4/(2*-1) = 2. Substituting x = 2 into the equation gives y = 4(2) - (2)² = 4. Therefore, the vertex is at the point (2, 4).
-
x-intercepts: The x-intercepts are the points where the parabola intersects the x-axis (where y = 0). To find them, we set y = 0 and solve for x: 0 = 4x - x². Factoring this equation gives 0 = x(4 - x). This yields two solutions: x = 0 and x = 4. Therefore, the x-intercepts are (0, 0) and (4, 0).
-
y-intercept: The y-intercept is the point where the parabola intersects the y-axis (where x = 0). Substituting x = 0 into the equation gives y = 4(0) - (0)² = 0. Therefore, the y-intercept is (0, 0). Notice that in this case, the y-intercept is the same as one of the x-intercepts.
-
Axis of Symmetry: The axis of symmetry is a vertical line that divides the parabola into two symmetrical halves. It passes through the vertex. The equation of the axis of symmetry is given by x = -b/(2a), which is x = 2 in this case.
-
Concavity: Since the coefficient of the x² term (a) is negative (-1), the parabola opens downwards. This means it has a maximum value at its vertex.
Sketching the Graph
Now that we've identified the key features, we can sketch the graph of y = 4x - x².
-
Plot the vertex: Mark the point (2, 4) on the coordinate plane.
-
Plot the intercepts: Mark the points (0, 0) and (4, 0) on the coordinate plane.
-
Draw the axis of symmetry: Draw a vertical line passing through the vertex at x = 2.
-
Sketch the parabola: Draw a smooth curve that passes through the vertex and intercepts, remembering that the parabola opens downwards and is symmetrical about the axis of symmetry (x=2).
Analyzing the Graph
The graph visually represents the relationship between x and y defined by the equation y = 4x - x². Several observations can be made:
-
Maximum Value: The parabola reaches its maximum value at the vertex (2, 4). This means that the function y = 4x - x² has a maximum value of 4.
-
Domain and Range: The domain of the function (all possible x-values) is all real numbers (-∞, ∞). The range of the function (all possible y-values) is (-∞, 4].
-
Increasing and Decreasing Intervals: The function is increasing for x < 2 and decreasing for x > 2.
-
Symmetry: The parabola exhibits symmetry around the vertical line x = 2.
Applications and Extensions
The quadratic function y = 4x - x² has applications in various fields:
-
Projectile Motion: In physics, this type of equation can model the trajectory of a projectile, where x represents the horizontal distance and y represents the vertical height. The vertex represents the maximum height reached by the projectile.
-
Optimization Problems: Finding the maximum value of the function is crucial in optimization problems. For instance, this equation could represent the profit function of a business, where x represents the number of units produced, and y represents the profit. The vertex would indicate the number of units that maximize profit.
-
Area and Geometry: The equation can represent the area of a rectangle with a specific relationship between its sides.
Further Exploration: Calculus
Using calculus, we can further analyze the function:
-
Derivative: The derivative of y = 4x - x² is dy/dx = 4 - 2x. Setting the derivative to zero (4 - 2x = 0) gives x = 2, confirming the x-coordinate of the vertex. The second derivative, d²y/dx² = -2, is negative, indicating that the function is concave down, consistent with our observation.
-
Integration: Integrating the function allows us to calculate the area under the curve. This has applications in determining various quantities related to the area represented by the parabola.
Transformations and Variations
By modifying the equation, we can explore transformations of the parabola:
-
Vertical Shift: Adding a constant to the equation shifts the parabola vertically. For example, y = 4x - x² + 3 shifts the parabola upwards by 3 units.
-
Horizontal Shift: Replacing x with (x - h) shifts the parabola horizontally by h units. For example, y = 4(x - 1) - (x - 1)² shifts the parabola one unit to the right.
-
Vertical Stretch/Compression: Multiplying the entire equation by a constant stretches or compresses the parabola vertically.
Understanding these transformations enhances the ability to manipulate and interpret quadratic functions.
Conclusion
The graph of y = 4x - x² offers a rich illustration of a fundamental mathematical concept. By analyzing its vertex, intercepts, axis of symmetry, and concavity, we gain a comprehensive understanding of its characteristics. Its application in various fields, including physics, economics, and geometry, highlights its practical significance. Furthermore, employing calculus provides even deeper insights into its behavior and properties. This detailed analysis serves as a foundation for exploring more complex mathematical relationships and functions. The ability to readily sketch and interpret this type of graph is a crucial skill for students and professionals alike in numerous quantitative fields.
Latest Posts
Latest Posts
-
Is Boiling Point Chemical Or Physical
Apr 06, 2025
-
What Is 4 66666 As A Fraction
Apr 06, 2025
-
How Many Inches Is 1 4
Apr 06, 2025
-
How To Find N In A Geometric Sequence
Apr 06, 2025
-
What Is Molar Mass Of Iron
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Graph Of Y 4x X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
