Gcf Of 18 36 And 45
listenit
May 25, 2025 · 5 min read
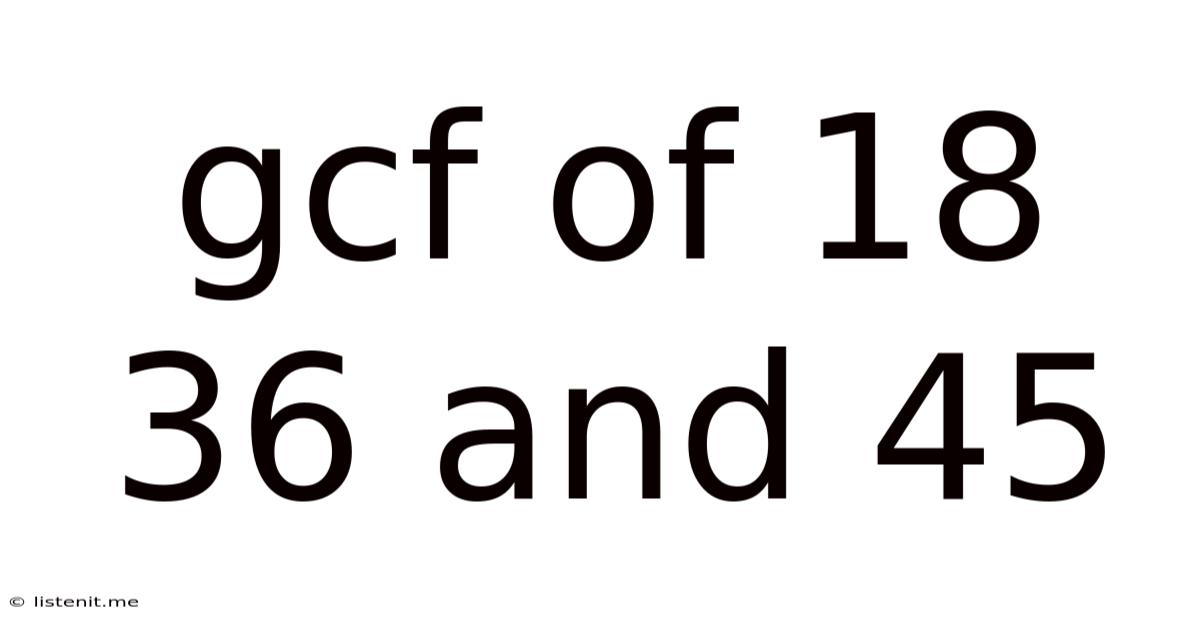
Table of Contents
Finding the Greatest Common Factor (GCF) of 18, 36, and 45: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of a set of numbers is a fundamental concept in mathematics with applications across various fields, from simplifying fractions to solving algebraic equations. This comprehensive guide will delve into the process of determining the GCF of 18, 36, and 45, exploring multiple methods and highlighting the underlying mathematical principles. We'll also examine the practical significance of GCF and its broader relevance in mathematics and beyond.
Understanding the Greatest Common Factor (GCF)
The GCF of a set of numbers is the largest number that divides each of the numbers in the set without leaving a remainder. It's the highest common factor shared by all the numbers. Understanding this definition is crucial before we proceed to calculate the GCF of 18, 36, and 45.
Why is Finding the GCF Important?
The GCF has several practical applications:
-
Simplifying Fractions: The GCF allows us to simplify fractions to their lowest terms. For example, if we have the fraction 18/36, finding the GCF (which is 18) allows us to simplify it to 1/2.
-
Solving Algebraic Equations: The GCF plays a vital role in factoring algebraic expressions, making it easier to solve equations.
-
Real-World Applications: GCF is used in various real-world scenarios, such as dividing objects into equal groups, determining the dimensions of objects, and in many areas of engineering and design.
Methods for Finding the GCF of 18, 36, and 45
There are several effective methods to calculate the GCF. Let's explore the most common ones, applying them to find the GCF of 18, 36, and 45.
Method 1: Listing Factors
This method involves listing all the factors of each number and identifying the largest factor common to all three.
Factors of 18: 1, 2, 3, 6, 9, 18 Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36 Factors of 45: 1, 3, 5, 9, 15, 45
Comparing the lists, we find that the common factors are 1, 3, and 9. The largest of these is 9. Therefore, the GCF of 18, 36, and 45 is 9.
This method is straightforward for smaller numbers but can become cumbersome when dealing with larger numbers with many factors.
Method 2: Prime Factorization
This method involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
Prime Factorization of 18: 2 x 3 x 3 = 2 x 3² Prime Factorization of 36: 2 x 2 x 3 x 3 = 2² x 3² Prime Factorization of 45: 3 x 3 x 5 = 3² x 5
The common prime factors are 3. The lowest power of 3 present in all factorizations is 3². Therefore, the GCF is 3² = 9.
This method is more efficient than listing factors, especially for larger numbers. It provides a systematic approach and is less prone to errors.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a particularly efficient method for finding the GCF of two numbers. It can be extended to find the GCF of more than two numbers by finding the GCF of the first two numbers and then finding the GCF of the result and the third number, and so on.
Let's apply it to 18, 36, and 45:
-
Find the GCF of 18 and 36: Divide 36 by 18: 36 ÷ 18 = 2 with a remainder of 0. The GCF of 18 and 36 is 18.
-
Find the GCF of 18 and 45: Divide 45 by 18: 45 ÷ 18 = 2 with a remainder of 9. Now divide 18 by the remainder 9: 18 ÷ 9 = 2 with a remainder of 0. The GCF of 18 and 45 is 9.
Therefore, the GCF of 18, 36, and 45 is 9.
The Euclidean algorithm is highly efficient, especially for large numbers, as it avoids the need to find all factors.
Further Exploration of GCF and Related Concepts
Understanding the GCF lays the groundwork for grasping other crucial mathematical concepts:
Least Common Multiple (LCM)
The least common multiple (LCM) is the smallest number that is a multiple of all the numbers in a given set. The LCM and GCF are related by the following formula:
LCM(a, b) x GCF(a, b) = a x b
This formula holds true for two numbers, 'a' and 'b'. For more than two numbers, the calculation becomes slightly more complex but follows a similar principle.
For our example, the LCM of 18, 36, and 45 can be calculated using prime factorization or other methods. Knowing the GCF (9) helps simplify the LCM calculation.
Applications in Different Mathematical Areas
The GCF and LCM have applications in various areas of mathematics including:
-
Number Theory: Exploring the properties of numbers, prime numbers, and their relationships.
-
Algebra: Factoring polynomials, simplifying expressions, and solving equations.
-
Geometry: Calculating dimensions, areas, and volumes, particularly in problems involving similar figures.
-
Fraction Operations: Simplifying fractions and performing operations like addition and subtraction of fractions with different denominators.
Advanced Concepts Related to GCF and LCM
For advanced learners, further exploration could include:
-
Bézout's Identity: This theorem states that for any two integers, 'a' and 'b', there exist integers 'x' and 'y' such that ax + by = GCF(a, b).
-
Modular Arithmetic: GCF plays a role in understanding congruences and solving equations in modular arithmetic.
-
Abstract Algebra: The concept of GCF extends to more abstract algebraic structures.
Conclusion
Determining the GCF of 18, 36, and 45, as demonstrated through various methods, is a fundamental skill with wide-ranging applications across mathematics and beyond. Understanding the different approaches, from listing factors to utilizing the Euclidean algorithm, allows you to choose the most efficient method based on the numbers involved. Mastering GCF and related concepts like LCM opens doors to more advanced mathematical concepts and problem-solving techniques. The seemingly simple task of finding the GCF underlies a rich and complex area of mathematical study with far-reaching practical implications. By understanding these principles, you are better equipped to tackle more complex mathematical challenges and apply these skills in various real-world scenarios.
Latest Posts
Latest Posts
-
C Cup Breast Size In Inches
May 25, 2025
-
3 5 Divided By 6 7
May 25, 2025
-
1966 To 2023 How Many Years
May 25, 2025
-
How To Measure A Tire Height
May 25, 2025
-
How Long Has It Been Since 11 30
May 25, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 18 36 And 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.