Five Times The Square Of A Number
listenit
May 10, 2025 · 6 min read
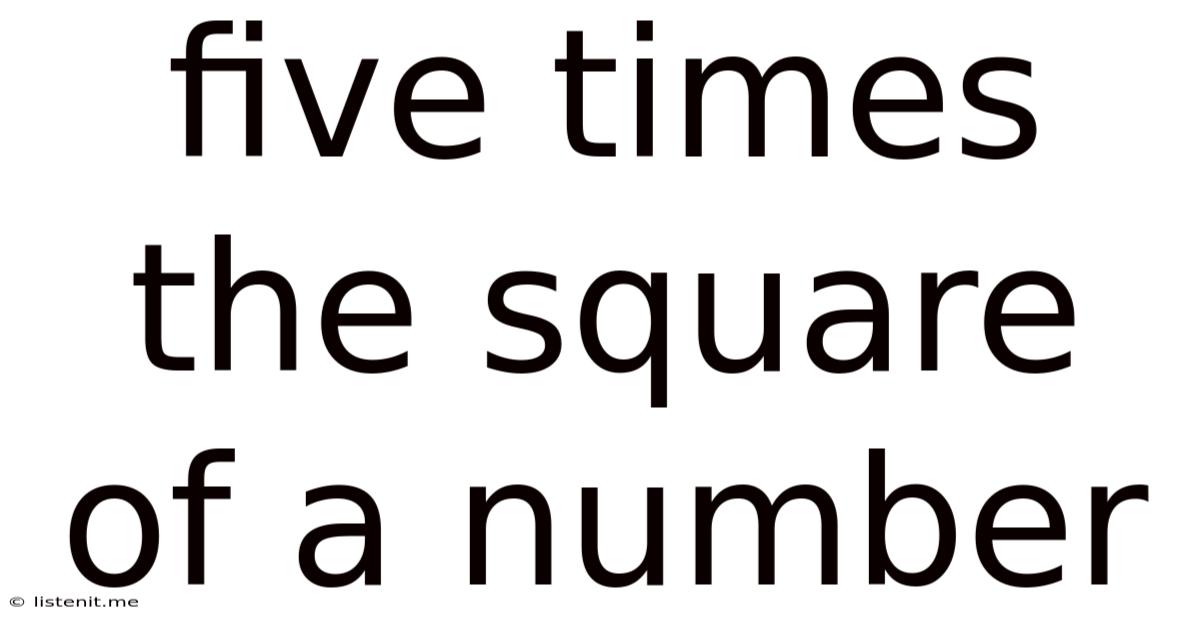
Table of Contents
Five Times the Square of a Number: A Deep Dive into Mathematical Concepts and Applications
The seemingly simple phrase "five times the square of a number" hides a wealth of mathematical richness, encompassing various algebraic concepts, problem-solving techniques, and real-world applications. This exploration delves into the intricacies of this expression, examining its fundamental structure, exploring its representation in different forms, and illustrating its usage in diverse contexts. We'll unravel its meaning, explore its properties, and discover its surprising relevance in fields beyond pure mathematics.
Understanding the Core Concept
At its heart, the expression "five times the square of a number" represents a specific mathematical operation. Let's break it down step-by-step:
-
A number: This represents an arbitrary value, often denoted by a variable like 'x' or 'n'. It could be any real number – positive, negative, or zero.
-
The square of a number: This refers to the number multiplied by itself (n * n or n²). Squaring a number geometrically represents the area of a square with sides of that length.
-
Five times the square: This involves multiplying the result of the squaring operation by five (5 * n²).
Therefore, the entire expression, "five times the square of a number," can be concisely represented algebraically as 5n². This simple equation forms the foundation for numerous mathematical explorations and practical applications.
Algebraic Representation and Manipulation
The algebraic representation, 5n², allows us to perform various mathematical manipulations. For instance, we can:
-
Evaluate the expression for specific values of 'n': If n = 2, then 5n² = 5(2²) = 5(4) = 20. If n = -3, then 5n² = 5(-3)² = 5(9) = 45. Note that the result is always positive, regardless of whether 'n' is positive or negative, due to the squaring operation.
-
Solve equations involving the expression: Consider the equation 5n² = 80. To solve for 'n', we divide both sides by 5: n² = 16. Taking the square root of both sides gives n = ±4 (both 4 and -4 satisfy the equation).
-
Graph the expression: Plotting 5n² on a Cartesian coordinate system results in a parabola, a U-shaped curve that opens upwards. This visual representation highlights the quadratic nature of the expression. The parabola's vertex is at the origin (0,0), demonstrating that the minimum value of the expression is 0, which occurs when n = 0.
-
Expand and factor expressions containing 5n²: If the expression is part of a larger algebraic equation, techniques like expanding brackets or factoring can simplify the equation and facilitate solving. For example, expanding (n + 2)(5n² - 3) would require the distributive property.
Geometric Interpretation
The expression 5n² has a clear geometric interpretation. Imagine a square with sides of length 'n'. Its area is n². Now, imagine five such squares arranged together. The total area of these five squares would be 5n², directly representing the value of our expression. This visual representation helps to solidify the understanding of the expression's meaning and can be particularly helpful in visualizing problem-solving approaches.
Real-World Applications
The seemingly abstract concept of "five times the square of a number" finds surprisingly diverse applications in the real world:
Physics:
-
Calculating Kinetic Energy: Kinetic energy, the energy an object possesses due to its motion, is directly proportional to the square of its velocity. If a constant factor is involved (such as in a specific scenario with consistent mass), the formula might resemble 5v², where 'v' represents velocity.
-
Analyzing Projectile Motion: The distance a projectile travels horizontally can often involve a quadratic relationship, potentially incorporating a factor like 5, depending on the specific scenario and units used.
Engineering:
-
Calculating Structural Strength: In structural engineering, the strength of certain materials might be related to the square of a dimension (like the cross-sectional area of a beam), resulting in calculations involving expressions similar to 5n².
-
Analyzing Electrical Circuits: Power dissipation in electrical circuits often involves the square of current, leading to equations where a constant factor, similar to 5, might be present.
Finance:
- Compound Interest: Although the standard compound interest formula doesn't directly involve '5n²', the exponential growth inherent in compound interest exhibits a quadratic-like increase over time, especially in scenarios with significant initial investments or high interest rates.
Everyday Life:
-
Area Calculations: Suppose you're tiling a floor. If each tile has an area represented by n², and you need five times that amount, the total area becomes 5n².
-
Cooking: Consider a recipe where the cooking time is proportional to the square of the amount of food being cooked (perhaps due to increased cooking time needed for larger volumes). If you adjust the recipe to use five times the ingredients, the cooking time might be calculated using a similar expression.
Advanced Mathematical Concepts and Extensions
Beyond the basic understanding and applications discussed above, the expression 5n² can serve as a springboard into more advanced mathematical concepts:
-
Calculus: Derivatives and integrals involving 5n² are straightforward to compute, contributing to applications in optimization problems, calculating areas under curves, and solving differential equations.
-
Linear Algebra: The expression could be incorporated into matrix operations or vector calculations, depending on the context.
-
Number Theory: Investigating the properties of numbers that yield integer solutions for 5n² can lead to explorations of prime numbers, perfect squares, and other number-theoretic concepts.
-
Abstract Algebra: The expression can be generalized and studied within abstract algebraic structures, enabling explorations of group theory, ring theory, or field theory.
Problem-Solving Techniques
To effectively utilize the expression 5n² in problem-solving, consider these strategies:
-
Clearly define the variable 'n': Identify what 'n' represents in the context of the problem.
-
Translate the problem into an equation: Express the problem's conditions using the expression 5n² and other relevant mathematical relationships.
-
Solve the equation: Employ appropriate algebraic techniques to solve for 'n' or any other unknown variable.
-
Interpret the solution: Ensure that the solution makes sense within the context of the problem.
Conclusion
The expression "five times the square of a number," while seemingly simple, encapsulates fundamental mathematical concepts and finds practical applications across various fields. Understanding its algebraic representation, geometric interpretation, and diverse applications expands mathematical literacy and empowers problem-solving abilities. Its exploration opens doors to further mathematical learning and deepens appreciation for the interconnectedness of mathematical ideas within both theoretical and practical contexts. From calculating areas to understanding physical phenomena, the seemingly simple 5n² reveals its power and relevance in unexpected and rewarding ways. By mastering this foundational concept, you equip yourself with a valuable tool for navigating the world of mathematics and its diverse applications.
Latest Posts
Latest Posts
-
1 And 7 8 As An Improper Fraction
May 10, 2025
-
Which Missing Item Would Complete This Beta Decay Reaction
May 10, 2025
-
What Is The Oxidation Number Of Fe In Fe2o3
May 10, 2025
-
How To Calculate Second Ionization Energy
May 10, 2025
-
How Many Valence Electrons Do All Alkali Metals Have
May 10, 2025
Related Post
Thank you for visiting our website which covers about Five Times The Square Of A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.