Five Percent Of What Number Is 1.25
listenit
May 25, 2025 · 5 min read
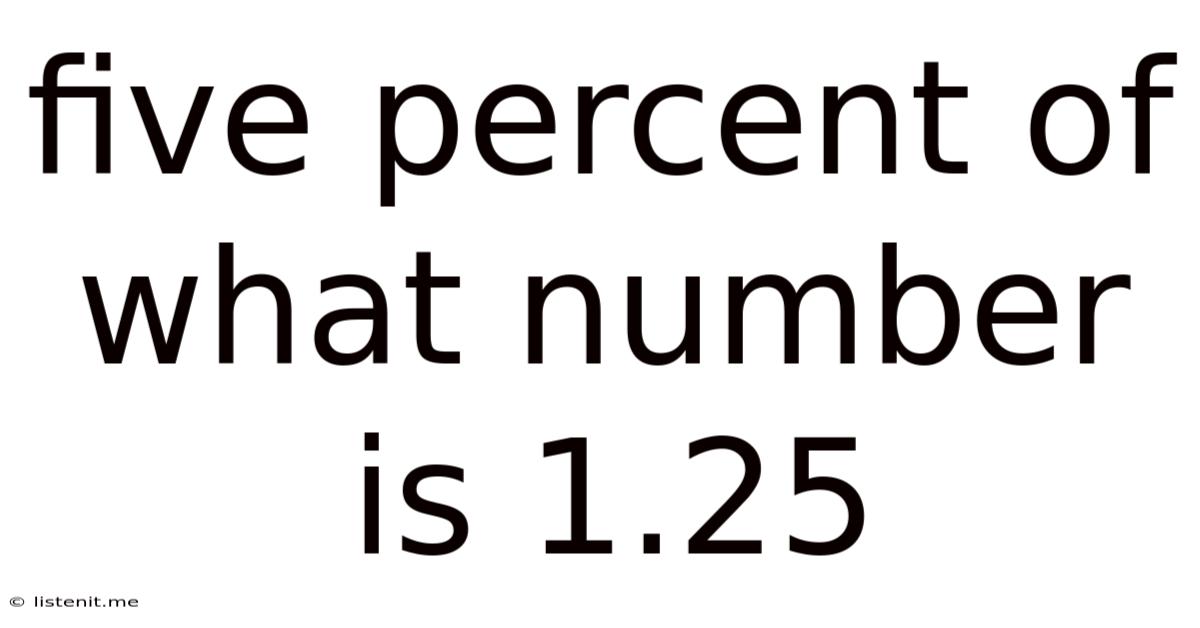
Table of Contents
Five Percent of What Number is 1.25? Unraveling the Math and its Applications
This seemingly simple question, "Five percent of what number is 1.25?", opens the door to a fascinating exploration of percentage calculations, their real-world applications, and the underlying mathematical principles. While the answer itself is straightforward to calculate, understanding the why behind the calculation is crucial for mastering percentages and applying this knowledge to various situations. This article will not only provide the solution but also delve into the methods, provide practical examples, and explore the broader implications of percentage calculations.
Understanding Percentages: The Foundation
Before we dive into the problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100". For example, 25% means 25 out of 100, which can also be written as the fraction 25/100 or the decimal 0.25.
This fundamental understanding is vital because percentage problems often involve translating word problems into mathematical equations. The words "of" usually represent multiplication, and "is" represents equality. This allows us to translate the problem into a solvable equation.
Solving the Problem: Five Percent of What Number is 1.25?
Our problem states: "Five percent of what number is 1.25?" Let's translate this into a mathematical equation:
0.05 * x = 1.25
Where:
- 0.05 represents 5% (5 divided by 100)
- x represents the unknown number we're trying to find.
- 1.25 is the result of 5% of x.
To solve for x, we use basic algebra:
-
Divide both sides of the equation by 0.05: This isolates x. x = 1.25 / 0.05
-
Perform the division: 1.25 divided by 0.05 equals 25.
Therefore, x = 25
Five percent of 25 is 1.25.
Alternative Methods: Different Approaches, Same Result
While the algebraic method is efficient, there are other ways to approach this problem. Let's explore a couple more:
Method 2: Using Proportions
We can set up a proportion to solve this problem:
5/100 = 1.25/x
This proportion states that the ratio of 5 to 100 is equal to the ratio of 1.25 to the unknown number (x). Cross-multiplying gives us:
5x = 125
Dividing both sides by 5 gives us:
x = 25
Method 3: Working with Fractions
We can also express 5% as a fraction (5/100) and solve the equation:
(5/100) * x = 1.25
Multiply both sides by 100:
5x = 125
Divide both sides by 5:
x = 25
Real-World Applications: Percentage Calculations in Everyday Life
Understanding percentage calculations is essential for navigating everyday life. Here are some examples:
-
Sales and Discounts: Stores often advertise discounts as percentages. For example, a "20% off" sale means you pay 80% of the original price. Knowing how to calculate these discounts helps you determine the final price.
-
Taxes and Tips: Calculating sales tax or adding a tip to a restaurant bill involves percentage calculations. Understanding these calculations ensures you pay the correct amount.
-
Interest Rates: Interest rates on loans and investments are expressed as percentages. Understanding these percentages helps you compare different financial options and make informed decisions.
-
Financial Analysis: Percentage change is used extensively in financial analysis to track the performance of investments, businesses, and the economy. For example, calculating year-over-year growth or decline in revenue or profit often involves percentage changes.
-
Statistical Analysis: Percentages are used in data analysis and statistics to present data in a clear and understandable manner. This can range from analyzing survey results to interpreting scientific findings.
-
Scientific Applications: Percentages are used to express concentrations, ratios, and probabilities in many fields of science. Examples include analyzing chemical solutions, calculating the likelihood of an event, or understanding population demographics.
Expanding the Understanding: Beyond the Basic Calculation
While solving "Five percent of what number is 1.25?" is relatively straightforward, the problem provides a launching point for more complex percentage calculations. Consider these extensions:
-
Finding the Percentage Increase or Decrease: Suppose a quantity increases from 20 to 25. What is the percentage increase? This involves calculating the difference (5), dividing it by the original amount (20), and then multiplying by 100 to express it as a percentage (25%). Conversely, you can calculate the percentage decrease using a similar process.
-
Compound Interest: Compound interest involves earning interest not only on the principal amount but also on accumulated interest. This requires understanding exponential growth and involves more complex percentage calculations.
-
Percentage Points vs. Percentage Change: It's crucial to understand the difference between these two terms. A change from 10% to 15% is a 5 percentage point increase, but a 50% percentage increase (5/10 * 100%).
Mastering Percentages: Practice and Resources
The best way to master percentage calculations is through consistent practice. Work through various examples, including those involving more complex scenarios like compound interest or percentage changes. Many online resources, such as educational websites and practice apps, offer additional problems and explanations to help you refine your skills.
Conclusion: The Power of Percentage Calculations
The seemingly simple problem of "Five percent of what number is 1.25?" unveils a rich mathematical concept with extensive real-world applications. From everyday shopping to complex financial analyses, understanding and applying percentage calculations is a valuable skill that empowers individuals to make informed decisions and navigate numerous aspects of life effectively. By mastering the fundamentals and exploring various problem-solving methods, you can build a strong foundation in mathematics and confidently tackle a wide range of percentage-related challenges. Remember, consistent practice is key to mastering this essential skill.
Latest Posts
Latest Posts
-
What Is 1 10 Of 3 000
May 25, 2025
-
What Is 4 Weeks From Now
May 25, 2025
-
What Is 8 10 In Simplest Form
May 25, 2025
-
18 10 More Than A Number X Is Equal To 29 5
May 25, 2025
-
How Long Is 22 Months In Years
May 25, 2025
Related Post
Thank you for visiting our website which covers about Five Percent Of What Number Is 1.25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.