Find The Quotient And Remainder For 52 8
listenit
May 12, 2025 · 5 min read
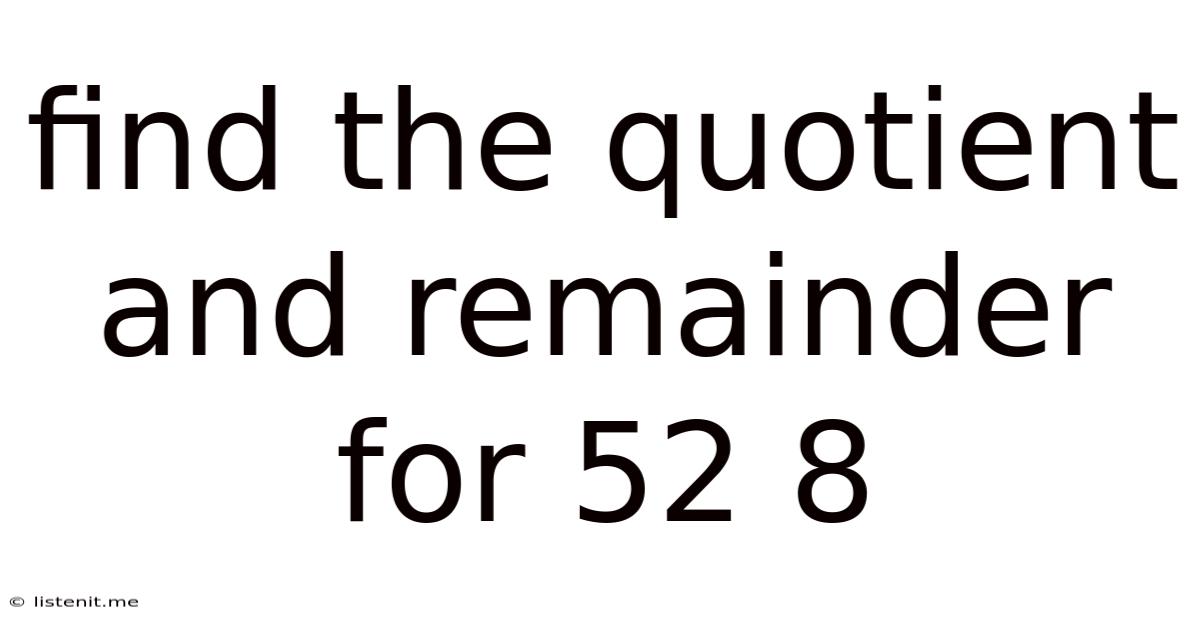
Table of Contents
Finding the Quotient and Remainder: A Deep Dive into Division
Division is a fundamental arithmetic operation, forming the bedrock of many mathematical concepts and real-world applications. Understanding how to find the quotient and remainder is crucial, especially when dealing with situations where a division doesn't result in a whole number. This article will provide a comprehensive exploration of this topic, encompassing various methods, practical examples, and applications. We will focus on finding the quotient and remainder for 52 divided by 8, but the principles discussed can be easily applied to any division problem.
Understanding the Basics: Quotient and Remainder
Before delving into the specifics of dividing 52 by 8, let's clarify the terminology. When we divide one number (the dividend) by another (the divisor), we obtain two key results:
- Quotient: This represents the number of times the divisor goes into the dividend completely. It's essentially the whole number result of the division.
- Remainder: This is the amount left over after the divisor has been divided into the dividend as many times as possible. The remainder is always smaller than the divisor.
Method 1: Long Division
Long division is a classic method for performing division, especially useful for larger numbers. Let's apply it to find the quotient and remainder for 52 ÷ 8:
-
Set up the problem: Write the dividend (52) inside the long division symbol and the divisor (8) outside.
_____ 8 | 52 -
Divide: How many times does 8 go into 5? It doesn't, so we move to the next digit. How many times does 8 go into 52? It goes in 6 times (6 x 8 = 48). Write the 6 above the 2 in the dividend.
6 _____ 8 | 52 -
Multiply: Multiply the quotient (6) by the divisor (8): 6 x 8 = 48. Write this result below the 52.
6 _____ 8 | 52 48 -
Subtract: Subtract the result (48) from the dividend (52): 52 - 48 = 4.
6 _____ 8 | 52 48 -- 4 -
Remainder: The result of the subtraction (4) is the remainder.
Therefore, when 52 is divided by 8, the quotient is 6 and the remainder is 4. We can express this as: 52 = 8 x 6 + 4.
Method 2: Repeated Subtraction
This method involves repeatedly subtracting the divisor from the dividend until the result is smaller than the divisor. Let's illustrate this for 52 ÷ 8:
-
Start with the dividend: Begin with the dividend, 52.
-
Repeatedly subtract the divisor:
- 52 - 8 = 44
- 44 - 8 = 36
- 36 - 8 = 28
- 28 - 8 = 20
- 20 - 8 = 12
- 12 - 8 = 4
-
Count the subtractions: We subtracted 8 six times before reaching a number smaller than 8 (which is 4). This number of subtractions (6) is the quotient.
-
The remaining number is the remainder: The remaining number, 4, is the remainder.
Again, we find that the quotient is 6 and the remainder is 4.
Method 3: Using Multiplication Tables (for smaller numbers)
For smaller division problems, you can use your knowledge of multiplication tables. You need to find the largest multiple of the divisor (8) that is less than or equal to the dividend (52).
We know that:
- 8 x 1 = 8
- 8 x 2 = 16
- 8 x 3 = 24
- 8 x 4 = 32
- 8 x 5 = 40
- 8 x 6 = 48
- 8 x 7 = 56
Since 48 is the largest multiple of 8 that is less than or equal to 52, the quotient is 6. The remainder is found by subtracting 48 from 52: 52 - 48 = 4.
Applications of Quotient and Remainder
The concept of quotient and remainder extends far beyond basic arithmetic. Here are some real-world applications:
-
Sharing Items: Imagine you have 52 candies to distribute equally among 8 friends. The quotient (6) tells you each friend gets 6 candies. The remainder (4) represents the candies left over.
-
Time Calculations: If a task takes 8 hours, and you have 52 hours available, the quotient (6) tells you can complete the task 6 times. The remainder (4) represents the remaining time.
-
Programming: Many programming languages use the modulo operator (%) to find the remainder of a division. This is incredibly useful in various algorithms and applications, such as determining if a number is even or odd, generating cyclical patterns, and more.
-
Measurement Conversions: Converting between units of measurement often involves finding quotients and remainders. For example, converting minutes to hours and minutes.
-
Scheduling and Allocation: Distributing resources, scheduling tasks, and optimizing workflows often involve considering quotients and remainders to ensure efficient allocation and minimal waste.
Understanding the Relationship: Dividend, Divisor, Quotient, and Remainder
The fundamental relationship between these four elements is expressed by the following equation:
Dividend = (Divisor x Quotient) + Remainder
In our example (52 ÷ 8):
52 = (8 x 6) + 4
This equation is always true for any division problem. It provides a powerful way to verify your results and deepen your understanding of the division process.
Expanding on the Concept: Larger Numbers and Decimal Divisions
The principles outlined above apply to division problems involving larger numbers as well. While the long division process might become more complex, the core concept of finding the quotient and remainder remains the same.
When dealing with decimal divisions (where the division doesn't result in a whole number), the quotient will contain a decimal part, and the remainder is typically expressed as a decimal fraction.
Conclusion
Finding the quotient and remainder is a vital skill in mathematics with numerous real-world applications. Mastering the techniques of long division, repeated subtraction, and utilizing multiplication tables provides a solid foundation for tackling various division problems. Understanding the relationship between the dividend, divisor, quotient, and remainder allows for verification and a deeper conceptual grasp of this fundamental arithmetic operation. Remember, the principles illustrated using 52 ÷ 8 can be applied to any division problem, regardless of the size of the numbers involved.
Latest Posts
Latest Posts
-
Why Is Filtration A Passive Process
May 12, 2025
-
Y 2x 3 Y 2x 1
May 12, 2025
-
What Is The Unit Of Measurement For Pressure
May 12, 2025
-
How To Find Percentage Abundance Of 3 Isotopes
May 12, 2025
-
Quadrilateral That Is Not A Rectangle
May 12, 2025
Related Post
Thank you for visiting our website which covers about Find The Quotient And Remainder For 52 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.