Find The Gcf Of 6 And 15
listenit
May 25, 2025 · 6 min read
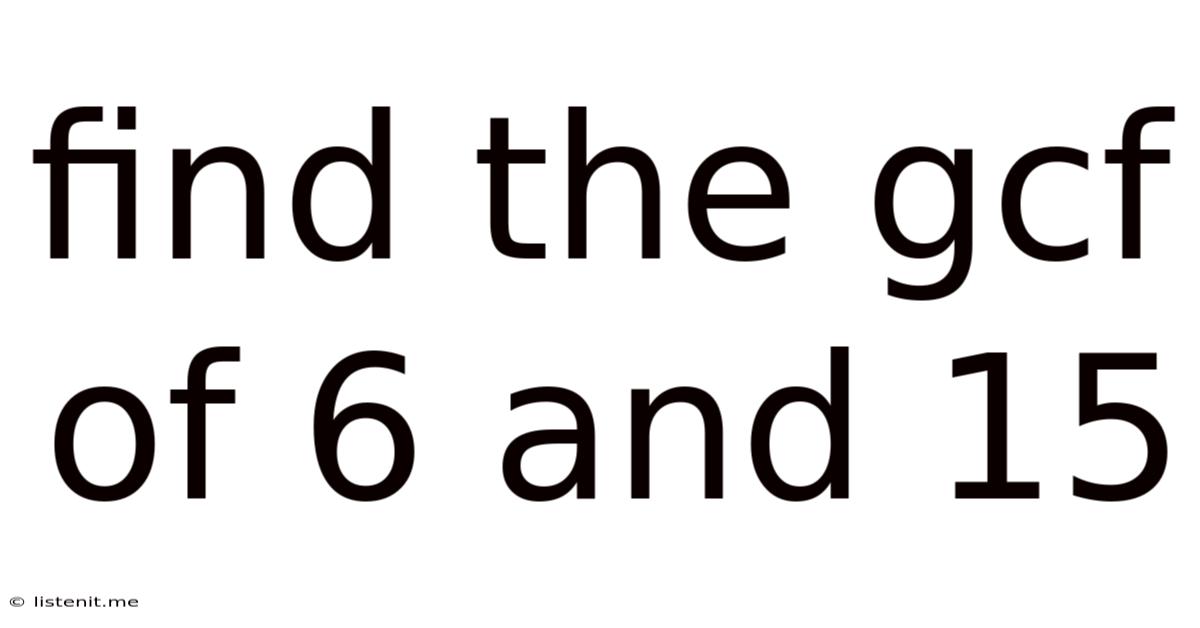
Table of Contents
Finding the Greatest Common Factor (GCF) of 6 and 15: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with applications across various fields, from simplifying fractions to solving algebraic equations. This comprehensive guide will delve into multiple methods for determining the GCF of 6 and 15, explaining the underlying principles and providing practical examples to solidify your understanding. We'll explore both simple and advanced techniques, ensuring you're equipped to tackle GCF problems of any complexity.
Understanding the Greatest Common Factor (GCF)
Before we jump into finding the GCF of 6 and 15, let's establish a clear understanding of what the GCF represents. The GCF of two or more numbers is the largest number that divides evenly into all of the given numbers without leaving a remainder. In essence, it's the biggest number that is a factor of all the numbers in question. This concept is crucial for simplifying fractions, factoring polynomials, and solving various mathematical problems.
Method 1: Listing Factors
This is the most straightforward method, particularly useful for smaller numbers like 6 and 15. We'll list all the factors of each number and then identify the largest factor they have in common.
Factors of 6:
The factors of 6 are the numbers that divide evenly into 6: 1, 2, 3, and 6.
Factors of 15:
The factors of 15 are: 1, 3, 5, and 15.
Identifying the GCF:
By comparing the lists, we see that the common factors of 6 and 15 are 1 and 3. The largest of these common factors is 3.
Therefore, the GCF of 6 and 15 is 3.
Method 2: Prime Factorization
Prime factorization involves expressing a number as the product of its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.). This method is more efficient for larger numbers and provides a systematic approach to finding the GCF.
Prime Factorization of 6:
6 can be expressed as 2 x 3. Both 2 and 3 are prime numbers.
Prime Factorization of 15:
15 can be expressed as 3 x 5. Both 3 and 5 are prime numbers.
Finding the GCF using Prime Factorization:
Once we have the prime factorization of both numbers, we identify the common prime factors and multiply them together to find the GCF. In this case, the only common prime factor of 6 and 15 is 3.
Therefore, the GCF of 6 and 15 is 3.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 6 and 15:
-
Start with the larger number (15) and the smaller number (6).
-
Divide the larger number (15) by the smaller number (6): 15 ÷ 6 = 2 with a remainder of 3.
-
Replace the larger number with the remainder (3). Now we have the numbers 6 and 3.
-
Repeat the process: Divide 6 by 3: 6 ÷ 3 = 2 with a remainder of 0.
-
Since the remainder is 0, the GCF is the last non-zero remainder, which is 3.
Therefore, the GCF of 6 and 15 is 3.
Applications of Finding the GCF
The ability to find the GCF is not merely an abstract mathematical exercise; it has numerous practical applications in various fields:
1. Simplifying Fractions:
The GCF plays a crucial role in simplifying fractions to their lowest terms. To simplify a fraction, we divide both the numerator and the denominator by their GCF. For example, the fraction 6/15 can be simplified by dividing both the numerator (6) and the denominator (15) by their GCF, which is 3: 6/15 = (6 ÷ 3) / (15 ÷ 3) = 2/5.
2. Factoring Polynomials:
Finding the GCF is a fundamental step in factoring polynomials. By identifying the GCF of the terms in a polynomial, we can factor it to simplify expressions and solve equations.
3. Solving Word Problems:
Many word problems involve finding the GCF to determine the largest possible equal groupings or divisions. For example, if you have 6 apples and 15 oranges, and you want to divide them into the largest possible equal groups with the same number of apples and oranges in each group, the GCF (3) tells you that you can create 3 groups, each containing 2 apples and 5 oranges.
4. Geometry and Measurement:
GCF is used in geometry when finding the dimensions of the largest square that can tile a rectangle with given dimensions. For instance, if you have a rectangle with dimensions 6 units by 15 units, the largest square that can perfectly tile this rectangle has sides of length equal to the GCF of 6 and 15, which is 3 units.
Advanced Techniques and Extensions
While the methods discussed above are sufficient for most GCF problems, more advanced techniques exist for dealing with larger numbers or multiple numbers:
-
Using a calculator or computer software: Many calculators and mathematical software packages have built-in functions to calculate the GCF efficiently.
-
The Least Common Multiple (LCM): The LCM and GCF are closely related. For two numbers a and b, the product of their GCF and LCM is equal to the product of the two numbers: GCF(a, b) * LCM(a, b) = a * b. This relationship can be used to find the LCM or GCF if one is known.
-
Extension to more than two numbers: The methods described (prime factorization and the Euclidean algorithm) can be extended to find the GCF of more than two numbers. For prime factorization, find the prime factorization of each number and identify the common prime factors with the lowest exponent. For the Euclidean algorithm, repeatedly apply the algorithm to pairs of numbers until you find the GCF of all the numbers.
Conclusion: Mastering the GCF
Finding the greatest common factor is a cornerstone of elementary number theory and has widespread applications in various mathematical and real-world contexts. Mastering the different methods—listing factors, prime factorization, and the Euclidean algorithm—equips you with the tools to tackle GCF problems efficiently and effectively, regardless of the numbers involved. Understanding the underlying concepts and practicing these methods will solidify your understanding and make you confident in applying this crucial mathematical skill. Remember to choose the method that best suits the complexity of the problem at hand, and always double-check your work to ensure accuracy.
Latest Posts
Latest Posts
-
What Is The Greatest Common Factor Of 48 And 20
May 25, 2025
-
How Many Days Since August 2
May 25, 2025
-
Greatest Common Factor Of 48 And 54
May 25, 2025
-
1978 To Now How Many Years
May 25, 2025
-
How To Measure For Tire Size
May 25, 2025
Related Post
Thank you for visiting our website which covers about Find The Gcf Of 6 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.