Find The Area Of The Triangle Below
listenit
Mar 27, 2025 · 5 min read
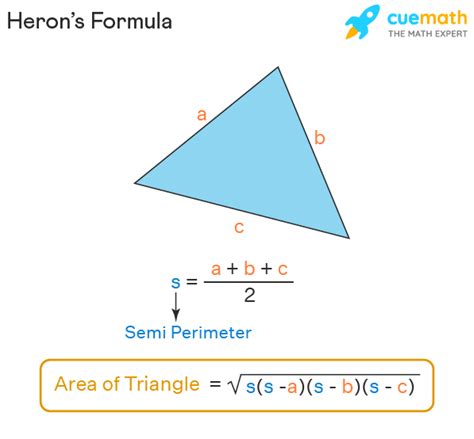
Table of Contents
Find the Area of a Triangle: A Comprehensive Guide
Finding the area of a triangle might seem like a simple task, especially if you remember the basic formula from school: ½ * base * height. However, determining the area becomes significantly more nuanced when dealing with different types of triangles and limited information. This comprehensive guide will delve into various methods for calculating the area of a triangle, addressing different scenarios and providing practical examples. We'll cover everything from the basic formula to more advanced techniques like Heron's formula and the use of trigonometry.
Understanding the Basic Formula: ½ * base * height
The most fundamental method for calculating the area of a triangle is using the formula: Area = ½ * base * height. This formula is applicable only when you know the length of the base and the corresponding height of the triangle.
- Base: The base is any one side of the triangle. You can choose any side as the base, but remember that the height must be perpendicular to the chosen base.
- Height: The height is the perpendicular distance from the vertex opposite the base to the base itself.
Example 1: Right-Angled Triangle
Let's say we have a right-angled triangle with a base of 6 cm and a height of 8 cm. Applying the formula:
Area = ½ * 6 cm * 8 cm = 24 cm²
This is a straightforward application of the formula.
Example 2: General Triangle
Consider a triangle where the base is 10 cm and the height is 5 cm. The calculation remains the same:
Area = ½ * 10 cm * 5 cm = 25 cm²
Remember, the height must always be perpendicular to the base. This is crucial, especially when dealing with triangles that aren't right-angled.
Heron's Formula: When Height is Unknown
Heron's formula provides a powerful method for calculating the area of a triangle when you know the lengths of all three sides (a, b, c) but not the height. It doesn't require knowing any angles.
First, calculate the semi-perimeter (s):
s = (a + b + c) / 2
Then, apply Heron's formula:
Area = √[s(s-a)(s-b)(s-c)]
Example 3: Using Heron's Formula
Let's say a triangle has sides of length a = 5 cm, b = 6 cm, and c = 7 cm.
-
Calculate the semi-perimeter: s = (5 + 6 + 7) / 2 = 9 cm
-
Apply Heron's formula:
Area = √[9(9-5)(9-6)(9-7)] = √[9 * 4 * 3 * 2] = √216 ≈ 14.7 cm²
Trigonometric Approach: Using Angles and Sides
Trigonometry offers another avenue for calculating the area of a triangle, particularly useful when you know two sides and the included angle. This method employs the formula:
Area = ½ * a * b * sin(C)
Where:
- a and b are the lengths of two sides.
- C is the angle between sides a and b.
Example 4: Using Trigonometry
Suppose we have a triangle with sides a = 10 cm and b = 8 cm, and the angle C between them is 60°.
Area = ½ * 10 cm * 8 cm * sin(60°) = 40 cm² * (√3 / 2) ≈ 34.6 cm²
Coordinate Geometry: Triangles on a Plane
If the vertices of the triangle are defined by their coordinates (x, y) on a Cartesian plane, we can utilize the determinant method to find the area. Given vertices A(x1, y1), B(x2, y2), and C(x3, y3), the area is:
Area = ½ |(x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2))|
The absolute value ensures a positive area.
Example 5: Using Coordinate Geometry
Let's say the vertices are A(1, 2), B(4, 6), and C(7, 2).
Area = ½ |(1(6 - 2) + 4(2 - 2) + 7(2 - 6))| = ½ |(4 + 0 - 28)| = ½ |-24| = 12 square units
Advanced Techniques and Applications
The methods outlined above represent the core techniques for finding the area of a triangle. However, more advanced scenarios and applications exist:
-
Triangles in Three Dimensions: Calculating the area of a triangle embedded within a three-dimensional space requires vector methods. The cross product of two vectors representing two sides of the triangle is used to find the area.
-
Calculus and Integration: For irregular or complex shapes that can be approximated by a series of triangles, calculus and integration techniques provide powerful tools for calculating the area.
-
Computer Graphics and Computer-Aided Design (CAD): The ability to accurately determine the area of triangles is fundamental in computer graphics and CAD software for rendering 3D models, calculating surface areas, and performing various geometric operations.
-
Real-World Applications: Area calculations for triangles have practical implications in surveying, architecture, engineering, and various fields where precise measurements are required.
Choosing the Right Method
The best method for calculating the area of a triangle depends entirely on the information available. Here’s a decision tree:
-
Do you know the base and height? If yes, use the formula ½ * base * height.
-
Do you know all three sides? If yes, use Heron's formula.
-
Do you know two sides and the included angle? If yes, use the trigonometric method.
-
Do you know the coordinates of the vertices? If yes, use the determinant method.
-
Other scenarios: Consider advanced techniques depending on the context and the information available.
Conclusion
Mastering the art of finding the area of a triangle involves understanding various methods and selecting the appropriate technique based on the given data. From the simple ½ * base * height formula to the more complex Heron's formula and trigonometric approaches, this guide has explored a range of techniques, equipping you with the knowledge to tackle a variety of triangle area problems. Remember to always carefully review the given information and select the most efficient and accurate method to achieve the desired result. The ability to precisely calculate the area of a triangle is not only a fundamental geometric skill but also a valuable tool with widespread practical applications.
Latest Posts
Latest Posts
-
How To Find Range Of Function Algebraically
Mar 30, 2025
-
What Is 1 2 3 4
Mar 30, 2025
-
What Type Of Rock Are Fossils Mostly Found In
Mar 30, 2025
-
During Which Phase Of Meiosis Do Homologous Chromosomes Separate
Mar 30, 2025
-
How Many Chromosomes Do Daughter Cells Have After Mitosis
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Find The Area Of The Triangle Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
