Factor The Expression Over The Complex Numbers. X2+36
listenit
May 12, 2025 · 5 min read
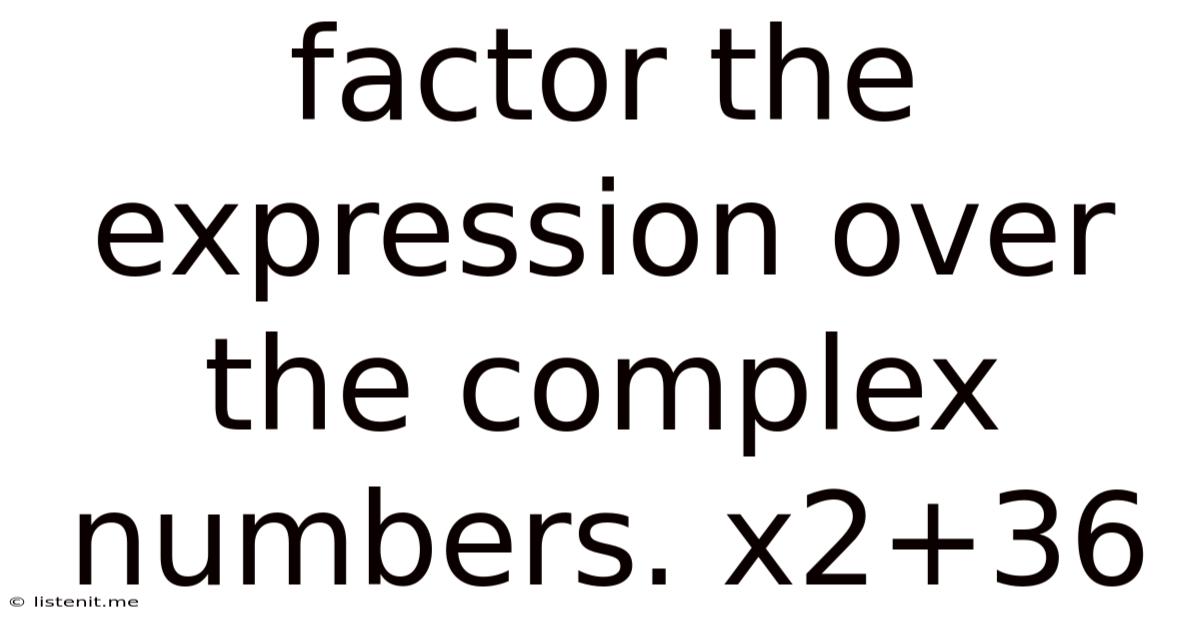
Table of Contents
Factoring the Expression x² + 36 Over the Complex Numbers: A Comprehensive Guide
Factoring quadratic expressions is a fundamental concept in algebra, crucial for solving equations and simplifying expressions. While real numbers often suffice, venturing into the realm of complex numbers unlocks a complete factorization for expressions that are unfactorable using only real numbers. This article delves into the process of factoring the expression x² + 36 over the complex numbers, providing a detailed explanation alongside illustrative examples and exploring the broader mathematical concepts involved.
Understanding Complex Numbers
Before diving into the factorization, let's refresh our understanding of complex numbers. Complex numbers extend the real number system by introducing the imaginary unit, denoted as 'i', where i² = -1. A complex number is typically expressed in the form a + bi, where 'a' and 'b' are real numbers, 'a' is the real part, and 'b' is the imaginary part.
Key Properties of Complex Numbers
- Addition and Subtraction: Complex numbers are added and subtracted by combining their real and imaginary parts separately. For example, (2 + 3i) + (4 - i) = (2 + 4) + (3 - 1)i = 6 + 2i.
- Multiplication: Complex numbers are multiplied using the distributive property (FOIL method), remembering that i² = -1. For instance, (2 + 3i)(4 - i) = 8 - 2i + 12i - 3i² = 8 + 10i + 3 = 11 + 10i.
- Conjugates: The conjugate of a complex number a + bi is a - bi. Multiplying a complex number by its conjugate always results in a real number: (a + bi)(a - bi) = a² + b². This property is crucial in many complex number manipulations.
Factoring x² + 36 over Real Numbers: An Impossibility
Attempting to factor x² + 36 using only real numbers proves unsuccessful. The expression lacks real roots because the discriminant (b² - 4ac) in the quadratic formula (for ax² + bx + c) is negative:
- a = 1, b = 0, c = 36
- Discriminant = 0² - 4 * 1 * 36 = -144
A negative discriminant indicates that the quadratic equation x² + 36 = 0 has no real solutions. Therefore, x² + 36 cannot be factored into linear expressions with real coefficients.
Factoring x² + 36 over Complex Numbers: The Solution
The key to factoring x² + 36 over complex numbers lies in recognizing that the expression is a difference of squares in disguise. We can rewrite it as:
x² - (-36)
Since -36 can be expressed as (6i)², we can now apply the difference of squares factorization formula (a² - b²) = (a + b)(a - b):
x² - (6i)² = (x + 6i)(x - 6i)
This factorization reveals the two complex roots of the equation x² + 36 = 0: x = -6i and x = 6i.
Verification Through Expansion
We can verify the correctness of our factorization by expanding the expression (x + 6i)(x - 6i):
(x + 6i)(x - 6i) = x² - 6ix + 6ix - (6i)² = x² - 36i² = x² + 36
The expansion yields the original expression, confirming the validity of our factorization.
Exploring Further: Applications and Significance
The ability to factor expressions over complex numbers has significant implications across various areas of mathematics and its applications:
1. Solving Polynomial Equations
Many polynomial equations, particularly those of higher degree, possess complex roots. Factoring over complex numbers provides a complete solution set, encompassing both real and complex roots. This is essential in fields like engineering and physics where complex solutions often represent physically meaningful quantities.
2. Signal Processing and Electrical Engineering
Complex numbers are fundamental to signal processing. Analyzing and manipulating signals often involves working with complex exponentials and Fourier transforms, which rely heavily on complex number factorization and manipulation techniques.
3. Quantum Mechanics
In quantum mechanics, complex numbers play a crucial role in describing the wave function of particles. Complex factorization techniques are used to solve the Schrödinger equation, which governs the behavior of quantum systems.
4. Advanced Algebra and Number Theory
Complex number factorization is central to abstract algebra and number theory. Concepts such as algebraic number fields and factorization in rings rely on the extension of number systems to encompass complex numbers.
Practical Examples: Applying the Concept
Let's consider a few examples to solidify our understanding:
Example 1: Factor y² + 100 over the complex numbers.
This is similar to our original problem. We can rewrite it as y² - (-100) = y² - (10i)². Applying the difference of squares formula, we get (y + 10i)(y - 10i).
Example 2: Solve the equation z² + 49 = 0 using complex numbers.
First, we rewrite the equation as z² = -49. Then, we factor -49 as (7i)². Thus, z² = (7i)², which implies z = ±7i. The solutions are z = 7i and z = -7i.
Example 3: Factor x⁴ + 81 over the complex numbers.
This is a more challenging example involving higher powers. We can treat it as a difference of squares by recognizing that x⁴ = (x²)² and 81 = (9)² = (3²)². Then we can write x⁴ + 81 = (x²)² - (9i²) = (x² - 9i)(x² + 9i). To factor further, we can use the difference of squares formula on each component, but they will be complex factors. For instance, to factor (x² - 9i), we might have to express -9i as a complex number squared and subsequently apply the difference of squares formula again. This demonstrates that even with higher-order polynomials, factorization using complex numbers still enables a complete breakdown into linear factors.
Conclusion: Embracing the Power of Complex Numbers
Factoring expressions like x² + 36 over the complex numbers unveils a richer understanding of quadratic equations and their solutions. While seemingly a simple algebraic manipulation, this process opens doors to a wider mathematical landscape, enabling the solution of equations previously unsolvable within the confines of real numbers. This extended capability extends far beyond theoretical mathematics and is crucial for solving problems in various scientific and engineering disciplines. Understanding and mastering this technique is essential for anyone seeking a deeper understanding of algebra and its applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about Factor The Expression Over The Complex Numbers. X2+36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.