Factor Completely 3x 2 7x 6
listenit
May 12, 2025 · 5 min read
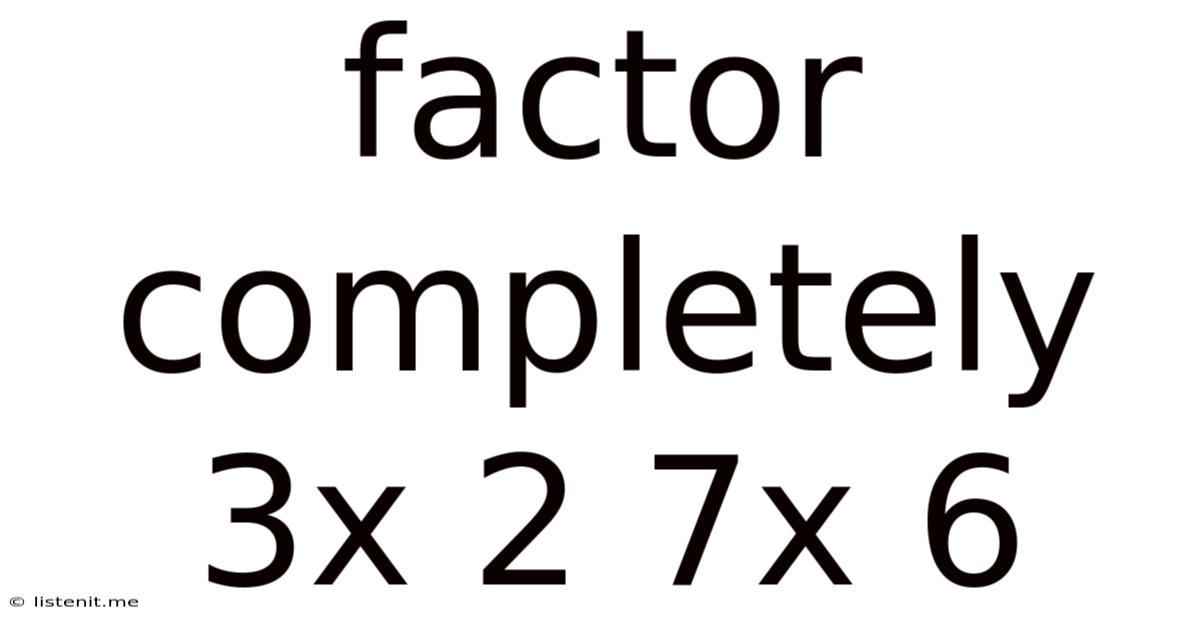
Table of Contents
Factoring Completely: A Deep Dive into 3x² + 7x - 6
Factoring quadratic expressions is a fundamental skill in algebra. It's a crucial stepping stone for solving equations, simplifying expressions, and understanding more advanced mathematical concepts. This article will provide a comprehensive guide to factoring the quadratic expression 3x² + 7x - 6, exploring various methods and highlighting important considerations along the way. We'll go beyond just finding the answer, delving into the underlying principles and providing you with the skills to tackle similar problems confidently.
Understanding Quadratic Expressions
Before we tackle the specific problem, let's review the general form of a quadratic expression: ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'x' is the variable. Our expression, 3x² + 7x - 6, fits this form, with a = 3, b = 7, and c = -6. The goal of factoring is to rewrite this expression as a product of two simpler expressions, typically two binomials.
Method 1: The AC Method (Product-Sum Method)
This method is a systematic approach to factoring quadratic expressions, especially useful when the leading coefficient (a) is not equal to 1. Here's how it works for 3x² + 7x - 6:
-
Find the product 'ac': In our case, a = 3 and c = -6, so ac = 3 * (-6) = -18.
-
Find two numbers that multiply to 'ac' and add up to 'b': We need two numbers that multiply to -18 and add up to 7. These numbers are 9 and -2 (9 + (-2) = 7 and 9 * (-2) = -18).
-
Rewrite the middle term: Replace the middle term (7x) with the two numbers we found, keeping the original coefficients of x: 3x² + 9x - 2x - 6.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
- 3x(x + 3) - 2(x + 3)
-
Factor out the common binomial: Notice that both terms now share the common binomial (x + 3). Factor it out:
- (x + 3)(3x - 2)
Therefore, the completely factored form of 3x² + 7x - 6 is (x + 3)(3x - 2).
Method 2: Trial and Error
This method involves a more intuitive approach, testing different combinations of binomial factors until you find the correct one. It's often faster for simpler quadratics but can be time-consuming for more complex expressions.
Since the leading coefficient is 3, the possible binomial factors will involve combinations of (3x ± ?) and (x ± ?). We need to find factors of -6 that, when combined with the outer and inner terms of the FOIL (First, Outer, Inner, Last) method, will add up to 7x.
Let's try some combinations:
- (3x + 1)(x - 6): This gives 3x² - 17x - 6 (incorrect)
- (3x - 1)(x + 6): This gives 3x² + 17x - 6 (incorrect)
- (3x + 2)(x - 3): This gives 3x² - 7x - 6 (incorrect)
- (3x - 2)(x + 3): This gives 3x² + 7x - 6 (correct!)
Again, we arrive at the factored form: (3x - 2)(x + 3). Note that the order of the factors doesn't matter; (x+3)(3x-2) is equivalent.
Method 3: Quadratic Formula
While not strictly a factoring method, the quadratic formula can help find the roots (or zeros) of the quadratic equation 3x² + 7x - 6 = 0. These roots can then be used to construct the factored form.
The quadratic formula is: x = [-b ± √(b² - 4ac)] / 2a
Plugging in our values (a = 3, b = 7, c = -6):
x = [-7 ± √(7² - 4 * 3 * -6)] / (2 * 3) x = [-7 ± √(49 + 72)] / 6 x = [-7 ± √121] / 6 x = [-7 ± 11] / 6
This gives us two solutions:
x₁ = (-7 + 11) / 6 = 4/6 = 2/3 x₂ = (-7 - 11) / 6 = -18/6 = -3
The roots are 2/3 and -3. We can use these roots to construct the factored form:
(x - 2/3)(x + 3) = 0
To get rid of the fraction, we can multiply the first factor by 3:
(3x - 2)(x + 3) = 0
This confirms our previous results.
Verifying the Factored Form
It's crucial to verify your factored form by expanding it using the FOIL method:
(3x - 2)(x + 3) = 3x² + 9x - 2x - 6 = 3x² + 7x - 6
This matches our original expression, confirming that (3x - 2)(x + 3) is the correct completely factored form.
Applications of Factoring
Factoring quadratic expressions has numerous applications in various fields:
-
Solving Quadratic Equations: Setting the factored expression equal to zero allows you to easily find the solutions (roots) of the corresponding quadratic equation.
-
Simplifying Algebraic Expressions: Factoring can simplify complex expressions, making them easier to manipulate and analyze.
-
Calculus: Factoring is essential in calculus for finding derivatives and integrals.
-
Physics and Engineering: Quadratic equations and their solutions frequently appear in physics and engineering problems involving projectile motion, oscillations, and other phenomena.
-
Computer Science: Factoring is used in algorithms and cryptography.
Advanced Factoring Techniques
While the methods above are sufficient for most quadratic expressions, more advanced techniques exist for factoring higher-degree polynomials or expressions with more complex coefficients. These include:
- Grouping: Used when there are four or more terms.
- Substitution: Replacing parts of an expression with a new variable to simplify the factoring process.
- Difference of Squares: a² - b² = (a + b)(a - b)
- Sum and Difference of Cubes: a³ + b³ = (a + b)(a² - ab + b²) and a³ - b³ = (a - b)(a² + ab + b²)
Conclusion
Factoring the quadratic expression 3x² + 7x - 6, whether using the AC method, trial and error, or the quadratic formula, ultimately leads to the same completely factored form: (3x - 2)(x + 3). Understanding these different methods and their underlying principles empowers you to tackle a wide range of factoring problems efficiently and confidently. Remember to always verify your results by expanding the factored form to ensure it matches the original expression. Mastering factoring is a cornerstone of algebraic proficiency, unlocking doors to more advanced mathematical concepts and applications in numerous fields.
Latest Posts
Latest Posts
-
How Much Is 1 2 A Quart
May 12, 2025
-
What Is 1 3 As A Whole Number
May 12, 2025
-
Is Oxygen A Waste Product Of Photosynthesis
May 12, 2025
-
What Percentage Of 40 Is 16
May 12, 2025
-
A Possible Explanation For A Set Of Observations
May 12, 2025
Related Post
Thank you for visiting our website which covers about Factor Completely 3x 2 7x 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.