Evaluate The Integral. 5 X2 + 25 Dx 0
listenit
May 10, 2025 · 5 min read
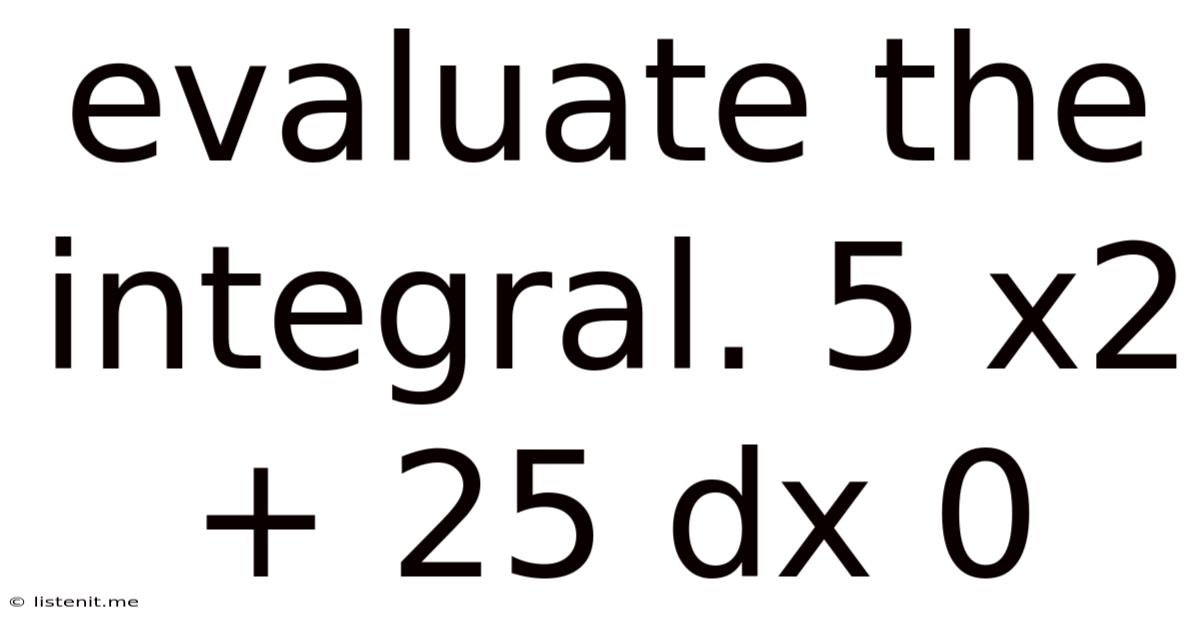
Table of Contents
Evaluating the Definite Integral: ∫₀⁵ (5x² + 25) dx
This article provides a comprehensive guide on how to evaluate the definite integral ∫₀⁵ (5x² + 25) dx. We'll break down the process step-by-step, explaining the fundamental concepts of integration and demonstrating the solution method. We'll also explore related concepts to enhance your understanding of integral calculus.
Understanding the Problem: Definite Integrals
The expression ∫₀⁵ (5x² + 25) dx represents a definite integral. This means we're finding the area under the curve of the function f(x) = 5x² + 25 between the limits of integration, x = 0 and x = 5. The limits 0 and 5 are crucial because they define the specific region whose area we're calculating. This contrasts with indefinite integrals, which produce a general antiderivative without specific limits.
Step-by-Step Solution: The Power Rule of Integration
To evaluate this definite integral, we'll employ the power rule of integration, a fundamental tool in calculus. The power rule states that the integral of xⁿ is (xⁿ⁺¹)/(n+1) + C, where n is any real number except -1, and C is the constant of integration (which becomes irrelevant in definite integrals).
1. Finding the Antiderivative:
First, we find the antiderivative of the integrand, 5x² + 25. We apply the power rule to each term separately:
- The antiderivative of 5x² is (5/3)x³ (because we increase the exponent by 1 and divide by the new exponent).
- The antiderivative of 25 (which is 25x⁰) is 25x (because the integral of a constant is the constant times x).
Therefore, the antiderivative of 5x² + 25 is (5/3)x³ + 25x. Note that we omit the constant of integration, C, because it cancels out when evaluating a definite integral.
2. Evaluating at the Limits of Integration:
Next, we evaluate the antiderivative at the upper and lower limits of integration (5 and 0, respectively). We subtract the value of the antiderivative at the lower limit from its value at the upper limit. This process is often represented as:
F(b) - F(a), where F(x) is the antiderivative, and 'a' and 'b' are the lower and upper limits, respectively.
In our case:
- F(5) = (5/3)(5)³ + 25(5) = (5/3)(125) + 125 = 625/3 + 125 = (625 + 375)/3 = 1000/3
- F(0) = (5/3)(0)³ + 25(0) = 0
3. Calculating the Definite Integral:
Finally, we subtract F(0) from F(5):
∫₀⁵ (5x² + 25) dx = F(5) - F(0) = 1000/3 - 0 = 1000/3
Therefore, the value of the definite integral ∫₀⁵ (5x² + 25) dx is 1000/3, or approximately 333.33. This represents the exact area under the curve of the function 5x² + 25 between x = 0 and x = 5.
Geometric Interpretation: Area Under the Curve
The definite integral ∫₀⁵ (5x² + 25) dx calculates the area of the region bounded by the curve y = 5x² + 25, the x-axis, and the vertical lines x = 0 and x = 5. This area is a combination of a rectangle and a region under a parabola. Visualizing this can help solidify your understanding of what the integral represents.
Expanding on Integration Techniques
While the power rule sufficed for this specific integral, let's briefly explore some other useful integration techniques:
1. U-Substitution:
U-substitution is a powerful technique for simplifying integrals by substituting a new variable, 'u', for a part of the integrand. This can transform complex integrals into simpler, more manageable forms. It's particularly helpful when dealing with composite functions.
2. Integration by Parts:
Integration by parts is a technique used to integrate the product of two functions. It's based on the product rule of differentiation and is especially useful when dealing with integrals involving products of functions like polynomials and exponentials or trigonometric functions.
3. Trigonometric Integrals:
Specific techniques exist for integrating trigonometric functions. These often involve trigonometric identities and substitutions to simplify the integrand.
4. Partial Fraction Decomposition:
Partial fraction decomposition is a method used to integrate rational functions (fractions where both the numerator and denominator are polynomials). It involves breaking down the rational function into simpler fractions that are easier to integrate.
Applications of Definite Integrals
Definite integrals have numerous applications across various fields:
-
Physics: Calculating work done by a variable force, finding the distance traveled by an object with varying velocity, and determining the center of mass of an object.
-
Engineering: Calculating areas and volumes of irregular shapes, analyzing stress and strain in materials, and modeling fluid flow.
-
Economics: Determining consumer surplus and producer surplus in markets, calculating total revenue and costs over time.
-
Probability and Statistics: Finding probabilities using probability density functions, calculating expected values, and working with continuous random variables.
Further Exploration: Numerical Integration
For integrals that are difficult or impossible to solve analytically (using the techniques discussed above), numerical integration methods provide approximations. These methods use numerical techniques to estimate the value of the definite integral. Common methods include:
- Trapezoidal Rule: Approximates the area under the curve using trapezoids.
- Simpson's Rule: Uses parabolas to approximate the area under the curve, providing generally better accuracy than the trapezoidal rule.
- Monte Carlo Integration: Uses random sampling to estimate the integral.
Conclusion: Mastering Definite Integrals
Evaluating definite integrals is a cornerstone of calculus, with far-reaching implications in various disciplines. Mastering the techniques discussed here – the power rule, and understanding more advanced methods like u-substitution and integration by parts – forms a strong foundation for tackling more complex mathematical problems. Remember that practice is key to building proficiency in integral calculus. By combining theoretical understanding with practical problem-solving, you'll develop a strong grasp of this essential mathematical concept. This article only scratches the surface; further exploration into advanced techniques and applications will significantly enhance your mathematical abilities and understanding.
Latest Posts
Latest Posts
-
The Variables X And Y Vary Inversely
May 10, 2025
-
Interconverting The Wavelength And Frequency Of Electromagnetic Radiation
May 10, 2025
-
40 As A Decimal And Fraction
May 10, 2025
-
What Is The Major Difference Between Primary And Secondary Succession
May 10, 2025
-
The Lanthanides And Actinides Belong Between
May 10, 2025
Related Post
Thank you for visiting our website which covers about Evaluate The Integral. 5 X2 + 25 Dx 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.