Does The Pythagorean Theorem Work For All Triangles
listenit
Apr 03, 2025 · 6 min read
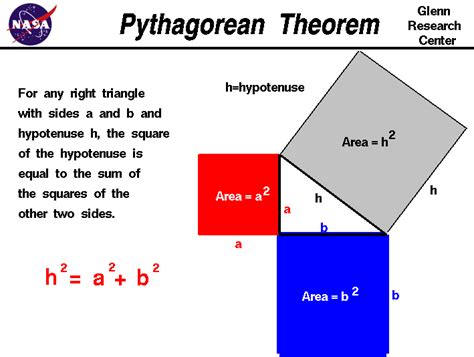
Table of Contents
Does the Pythagorean Theorem Work for All Triangles?
The Pythagorean Theorem, a cornerstone of geometry, states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (called legs or cathetus). This fundamental relationship, expressed as a² + b² = c², where 'a' and 'b' are the lengths of the legs and 'c' is the length of the hypotenuse, has far-reaching applications in various fields, from architecture and engineering to advanced mathematics and physics. But a crucial question arises: does this theorem hold true for all triangles? The simple answer is no. The Pythagorean Theorem is specifically and exclusively applicable to right-angled triangles. Let's delve deeper into why this is the case and explore the mathematical concepts that clarify its limitations.
Understanding the Pythagorean Theorem's Foundation
The Pythagorean Theorem is derived from the fundamental properties of right-angled triangles and their geometric relationships. Its proof can be demonstrated through various methods, including:
1. Geometric Proof using Squares:
This classic proof involves constructing squares on each side of the right-angled triangle. By manipulating the areas of these squares, it's demonstrably proven that the area of the square on the hypotenuse equals the sum of the areas of the squares on the other two sides. This visual demonstration solidifies the theorem's essence.
2. Algebraic Proof using Coordinate Geometry:
Using coordinate geometry, we can place the right-angled triangle on a Cartesian plane. By applying the distance formula between points, we can algebraically derive the Pythagorean Theorem. This method provides an analytical approach to proving the theorem's validity.
3. Trigonometric Proof:
Trigonometric functions, such as sine and cosine, can also be utilized to derive the Pythagorean Theorem. This method utilizes the relationships between angles and sides in a right-angled triangle.
These different proof methods highlight the inherent mathematical structure of right-angled triangles that underpins the theorem's validity. The relationship between the sides is intrinsically linked to the presence of the 90-degree angle. It's this specific angle that necessitates the precise relationship a² + b² = c².
Why the Pythagorean Theorem Fails for Other Triangles
The Pythagorean Theorem's applicability is strictly confined to right-angled triangles. The moment we deviate from a 90-degree angle, the relationship between the sides fundamentally changes. Let's examine why:
1. Acute Triangles:
In an acute triangle (all angles less than 90 degrees), the sum of the squares of the two shorter sides is greater than the square of the longest side. This is because the sides are proportionally shorter compared to a right-angled triangle with the same hypotenuse. The relationship can be expressed as a² + b² > c², where 'c' is the longest side.
2. Obtuse Triangles:
In an obtuse triangle (one angle greater than 90 degrees), the sum of the squares of the two shorter sides is less than the square of the longest side. The longer side opposite the obtuse angle becomes disproportionately larger. The relationship here is a² + b² < c², where 'c' is the longest side.
These inequalities demonstrate that the simple equality a² + b² = c² is only valid when the triangle contains a right angle. The angles of the triangle directly influence the proportional relationship between its sides, and only a 90-degree angle creates the precise balance expressed in the Pythagorean Theorem.
Exploring Alternative Laws for Non-Right Triangles
Since the Pythagorean Theorem doesn't apply to non-right triangles, we need alternative methods to determine side lengths and relationships. Two key laws emerge:
1. The Law of Cosines:
The Law of Cosines is a generalization of the Pythagorean Theorem applicable to any triangle. It relates the lengths of the sides to the cosine of one of the angles. The formula is:
c² = a² + b² - 2ab * cos(C)
where 'c' is the side opposite angle 'C'. When angle C is 90 degrees, cos(C) = 0, reducing the equation to the Pythagorean Theorem (c² = a² + b²).
2. The Law of Sines:
The Law of Sines describes the relationship between the lengths of the sides of a triangle and the sines of its opposite angles. The formula is:
a/sin(A) = b/sin(B) = c/sin(C)
This law is particularly useful when dealing with triangles where you know an angle and the opposite side.
Both the Law of Cosines and the Law of Sines are essential tools in solving problems involving triangles that are not right-angled. They effectively replace the Pythagorean Theorem in scenarios where its direct application is invalid.
Applications and Implications
The Pythagorean Theorem's limitations don't diminish its importance. Its specific application to right-angled triangles is crucial in numerous fields:
1. Navigation and Surveying:
Determining distances and locations using triangulation techniques heavily relies on the Pythagorean Theorem. Creating maps and navigating terrains often involves breaking down complex shapes into right-angled triangles for simplified calculations.
2. Construction and Engineering:
Calculating the diagonal lengths of structures, ensuring the stability and squareness of buildings, and designing supporting structures all utilize the Pythagorean Theorem to ensure accuracy and stability. It forms the basis of numerous construction calculations.
3. Computer Graphics and Game Development:
Creating realistic graphics and simulations necessitates precise calculations of distances and positions in 2D and 3D space. The Pythagorean Theorem is essential for calculating distances between points and determining positions of objects within these virtual environments.
4. Physics and Astronomy:
Calculating vectors, forces, and velocities in various physical systems relies on understanding the right-angled triangle relationships inherent in the Pythagorean Theorem. Its implications extend to complex physical modeling and simulations.
Even though the theorem is limited to right-angled triangles, its applications are widespread because many real-world problems can be broken down into simpler components that involve right-angled triangles.
Conclusion: Precision and Scope in Geometry
The Pythagorean Theorem is a powerful tool, but its power lies in its precise application to right-angled triangles. Understanding its limitations is as crucial as understanding its applications. While it doesn't directly work for all triangles, its principles are fundamental in the development of more generalized laws like the Law of Cosines and the Law of Sines, which are essential for solving problems involving all types of triangles. This highlights the importance of understanding the specific conditions and limitations of mathematical theorems and the elegance of mathematical generalizations that provide broader solutions. The fact that a simple theorem can have such profound implications underscores the beauty and utility of mathematical principles in our understanding of the world around us.
Latest Posts
Latest Posts
-
What Is Smaller Than A Cell
Apr 04, 2025
-
What Is 3 4 1 2
Apr 04, 2025
-
Words With The Root Word Hyper
Apr 04, 2025
-
What Is The Electron Configuration Of K
Apr 04, 2025
-
Is Pressure And Temperature Directly Proportional
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Does The Pythagorean Theorem Work For All Triangles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
