Derivative Of Sin 2x Cos 2x
listenit
May 10, 2025 · 5 min read
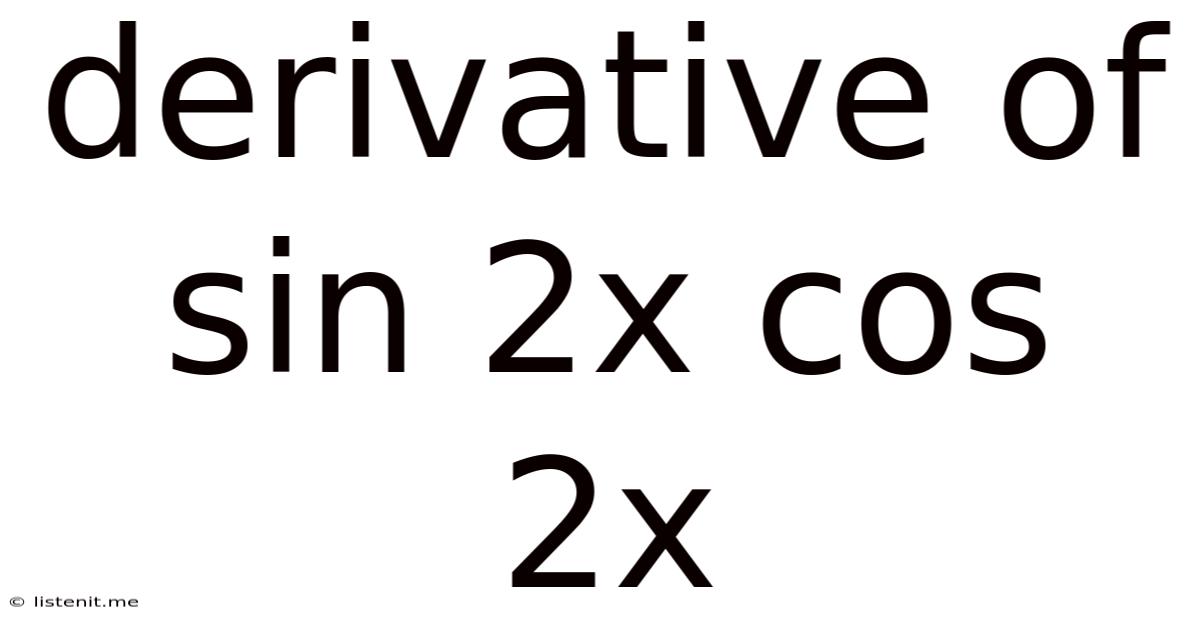
Table of Contents
Unveiling the Derivative of sin 2x cos 2x: A Comprehensive Guide
Finding the derivative of trigonometric functions often involves applying a combination of trigonometric identities and differentiation rules. The expression sin 2x cos 2x presents a perfect example of this. This comprehensive guide will walk you through various methods to derive the derivative, explaining each step in detail and highlighting key concepts along the way. We’ll explore the use of the product rule, double angle identities, and simplification techniques, ultimately leading to a clear and concise understanding of the solution.
Understanding the Fundamentals: Differentiation Rules and Trigonometric Identities
Before diving into the derivation, let's review the essential tools we'll be using:
1. The Product Rule
The product rule is a fundamental rule of calculus used to find the derivative of a product of two functions. If we have two differentiable functions, u(x) and v(x), then the derivative of their product is given by:
(d/dx)[u(x)v(x)] = u'(x)v(x) + u(x)v'(x)
This rule will be crucial in our derivation of the derivative of sin 2x cos 2x.
2. Key Trigonometric Identities
Several trigonometric identities will simplify our calculations. The most important ones for this problem are:
- Double Angle Identity for Sine: sin(2x) = 2sin(x)cos(x)
- Double Angle Identity for Cosine: cos(2x) = cos²(x) - sin²(x) = 1 - 2sin²(x) = 2cos²(x) - 1
- Pythagorean Identity: sin²(x) + cos²(x) = 1
Method 1: Applying the Product Rule Directly
The most straightforward approach involves applying the product rule directly to the expression sin 2x cos 2x. Let's break down the steps:
-
Identify u(x) and v(x): Let u(x) = sin 2x and v(x) = cos 2x.
-
Find the derivatives u'(x) and v'(x): Using the chain rule, we find the derivatives:
- u'(x) = d(sin 2x)/dx = cos 2x * d(2x)/dx = 2cos 2x
- v'(x) = d(cos 2x)/dx = -sin 2x * d(2x)/dx = -2sin 2x
-
Apply the product rule: Substituting into the product rule formula, we get:
(d/dx)[sin 2x cos 2x] = (2cos 2x)(cos 2x) + (sin 2x)(-2sin 2x)
-
Simplify the expression:
(d/dx)[sin 2x cos 2x] = 2cos² 2x - 2sin² 2x
-
Further simplification using double angle identity: Notice that the expression resembles the double angle identity for cosine. We can rewrite it as:
(d/dx)[sin 2x cos 2x] = 2(cos² 2x - sin² 2x) = 2cos 4x
Therefore, the derivative of sin 2x cos 2x is 2cos 4x.
Method 2: Using the Double Angle Identity for Sine
This method utilizes a trigonometric identity to simplify the expression before differentiation.
-
Apply the double angle identity: Recall that sin(2x) = 2sin(x)cos(x). While this identity doesn't directly apply to sin 2x cos 2x, let's consider a related expression. We know that sin(4x) = 2sin(2x)cos(2x). Therefore, sin(2x)cos(2x) = sin(4x)/2.
-
Differentiate the simplified expression: Now we differentiate sin(4x)/2 with respect to x:
(d/dx)[sin(4x)/2] = (1/2) * d(sin 4x)/dx = (1/2) * cos 4x * d(4x)/dx = (1/2) * 4cos 4x = 2cos 4x
This method provides a shorter and more elegant solution, showcasing the power of trigonometric simplification.
Method 3: A More Detailed Exploration Using the Chain Rule and Product Rule
Let's break down the application of the chain rule and product rule step-by-step, emphasizing the logic behind each step:
-
Product Rule Setup: We start by recognizing that we have a product of two functions: f(x) = sin(2x) and g(x) = cos(2x). The product rule states that the derivative of f(x)g(x) is f'(x)g(x) + f(x)g'(x).
-
Applying the Chain Rule: We need to find the derivatives f'(x) and g'(x). Since both functions are compositions of functions (a function of a function), we use the chain rule: d/dx [f(g(x))] = f'(g(x)) * g'(x).
-
Derivative of f(x) = sin(2x):
- The outer function is sin(u), where u = 2x.
- The derivative of sin(u) with respect to u is cos(u).
- The derivative of u (2x) with respect to x is 2.
- Therefore, f'(x) = cos(2x) * 2 = 2cos(2x).
-
Derivative of g(x) = cos(2x):
- The outer function is cos(u), where u = 2x.
- The derivative of cos(u) with respect to u is -sin(u).
- The derivative of u (2x) with respect to x is 2.
- Therefore, g'(x) = -sin(2x) * 2 = -2sin(2x).
-
Combining using the Product Rule: Now, we plug f'(x) and g'(x) into the product rule formula:
- d/dx [sin(2x)cos(2x)] = (2cos(2x))(cos(2x)) + (sin(2x))(-2sin(2x)) = 2cos²(2x) - 2sin²(2x)
-
Double Angle Identity for Cosine: Finally, we recognize that 2cos²(2x) - 2sin²(2x) is equivalent to 2[cos²(2x) - sin²(2x)], which is a double-angle identity for cosine: cos(4x).
- Therefore, d/dx [sin(2x)cos(2x)] = 2cos(4x).
Applications and Further Exploration
The derivative of sin 2x cos 2x, which simplifies to 2cos 4x, has applications in various fields, including:
- Physics: Describing oscillatory motion, particularly in systems involving harmonic oscillations. The function itself represents a sinusoidal wave, and its derivative represents the rate of change of that wave.
- Engineering: Modeling signal processing and wave phenomena. The derivative is critical in analyzing the frequency components of signals.
- Mathematics: Studying the properties of trigonometric functions and their applications in calculus and differential equations.
Further exploration could include:
- Higher-order derivatives: Finding the second, third, and higher-order derivatives of sin 2x cos 2x.
- Integration: Determining the indefinite and definite integrals of sin 2x cos 2x.
- Applications in other contexts: Exploring the role of this derivative in more complex mathematical models and real-world scenarios.
Conclusion
We've explored three different approaches to find the derivative of sin 2x cos 2x, each highlighting different techniques and emphasizing the importance of both differentiation rules and trigonometric identities. Understanding these methods provides a strong foundation for tackling more complex trigonometric derivatives and related problems in calculus and its applications. Remember to always break down complex problems into smaller, manageable steps and leverage the powerful tools provided by calculus and trigonometry. Through practice and careful attention to detail, mastery of these concepts becomes achievable.
Latest Posts
Latest Posts
-
What Is 38 Out Of 40
May 10, 2025
-
How To Calculate The Relative Abundance Of An Isotope
May 10, 2025
-
Whats The Prime Factorization Of 63
May 10, 2025
-
Are Zeros Before A Decimal Significant
May 10, 2025
-
Is The Square Root Of 64 Rational Or Irrational
May 10, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of Sin 2x Cos 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.