Derivative Of A Constant Is 0
listenit
May 12, 2025 · 6 min read
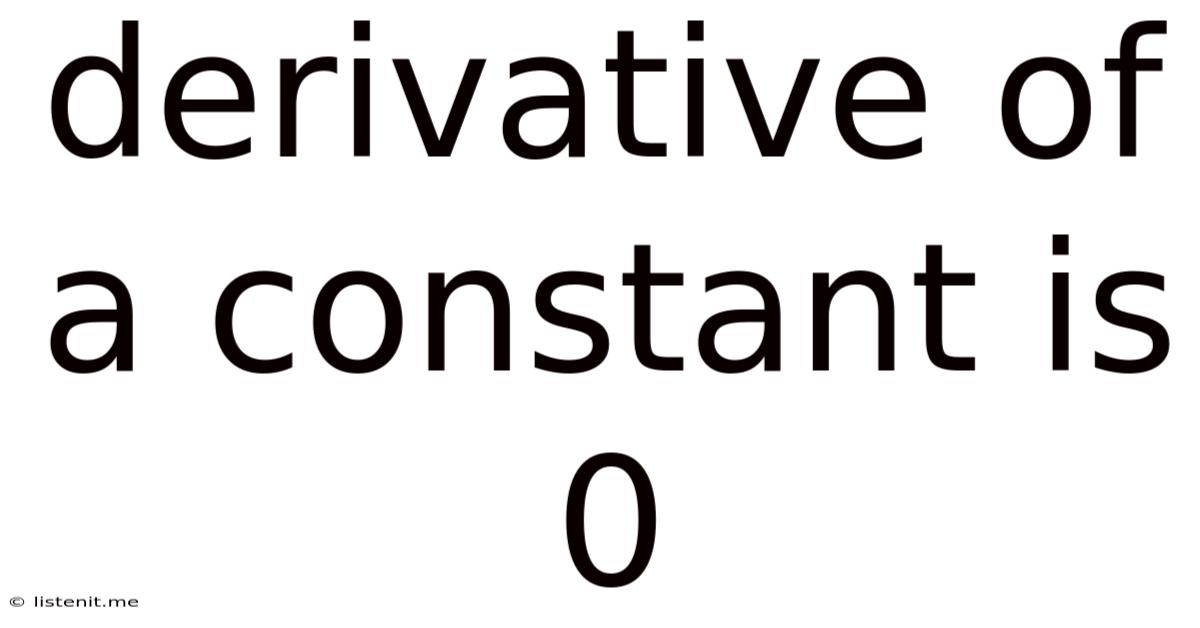
Table of Contents
The Derivative of a Constant is Zero: A Comprehensive Exploration
The statement "the derivative of a constant is zero" is a fundamental concept in calculus. Understanding why this is true is crucial for mastering differentiation and its applications in various fields, from physics and engineering to economics and finance. This article provides a comprehensive exploration of this concept, delving into its proof, implications, and practical applications.
Understanding Derivatives
Before diving into the specifics of constant derivatives, let's establish a firm understanding of what a derivative actually represents. In simple terms, the derivative of a function at a specific point measures the instantaneous rate of change of that function at that point. It essentially tells us how much the output of the function changes for a tiny change in the input. Geometrically, the derivative represents the slope of the tangent line to the function's graph at that point.
We often denote the derivative of a function f(x) with respect to x as f'(x) or df/dx. The process of finding the derivative is called differentiation.
Several methods exist for calculating derivatives, including:
-
The limit definition: This is the formal definition, defining the derivative as the limit of the difference quotient as the change in x approaches zero:
f'(x) = lim (h→0) [(f(x + h) - f(x)) / h] -
Power rule: This is a shortcut for differentiating power functions (functions of the form x<sup>n</sup>):
d/dx (x<sup>n</sup>) = nx<sup>n-1</sup> -
Sum/difference rule: The derivative of a sum or difference of functions is the sum or difference of their derivatives.
-
Product rule: Used for differentiating the product of two functions.
-
Quotient rule: Used for differentiating the quotient of two functions.
-
Chain rule: Used for differentiating composite functions (functions within functions).
Proving the Derivative of a Constant is Zero
Now, let's address the core topic: why the derivative of a constant is always zero. We can demonstrate this using the limit definition of the derivative.
Let's consider a constant function, denoted as f(x) = c, where 'c' is a constant (a fixed number). Applying the limit definition, we get:
f'(x) = lim (h→0) [(f(x + h) - f(x)) / h]
Since f(x) = c for all x, we can substitute this into the equation:
f'(x) = lim (h→0) [(c - c) / h]
This simplifies to:
f'(x) = lim (h→0) [0 / h]
Regardless of the value of h (as long as it's not zero), 0 divided by any non-zero number is always zero. Therefore:
f'(x) = 0
This proves that the derivative of any constant function is always zero. This result holds true for all values of x. The function's graph is a horizontal line, and the slope of a horizontal line is always zero, reinforcing the geometrical interpretation of the derivative.
Intuitive Explanation
Beyond the formal proof, we can also understand this intuitively. A constant function represents a quantity that does not change with respect to its input. The value of the function remains the same regardless of the input value. Since the derivative measures the rate of change, and the rate of change of a constant is zero, the derivative of a constant must also be zero. Think of a flat, horizontal line representing the constant function – its slope is zero everywhere.
Implications and Applications
The seemingly simple fact that the derivative of a constant is zero has significant implications and wide-ranging applications in various fields:
1. Simplifying Differentiation
When differentiating complex functions, often involving multiple terms and constants, understanding that the derivative of a constant is zero simplifies the process considerably. We can simply ignore the constant terms during differentiation, focusing only on the variable terms.
For example, consider the function:
f(x) = 3x² + 5x + 7
When differentiating, we only need to focus on the terms involving x:
f'(x) = 6x + 5
The constant term, 7, vanishes during differentiation.
2. Optimization Problems
In optimization problems, where we seek to find the maximum or minimum value of a function, the derivative plays a crucial role. Setting the derivative equal to zero helps identify critical points, which are potential locations of maxima or minima. The constant terms in the function don't affect the location of these critical points.
3. Physics and Engineering
In physics and engineering, many quantities are modeled as functions of time. The derivative represents the rate of change of these quantities. For instance, consider the position of an object as a function of time. If an object's position is constant (it's not moving), its velocity (the derivative of position with respect to time) is zero.
4. Economics and Finance
In economics, marginal cost and marginal revenue are crucial concepts. These are essentially derivatives of the total cost and total revenue functions, respectively. If there are fixed costs in a production process (represented as a constant), they won't affect the marginal cost, which only considers the change in costs with respect to the change in output.
5. Machine Learning
In machine learning, particularly in gradient descent algorithms used for optimizing models, the derivative guides the optimization process. Constants in the loss function, representing factors that don't change during training, won't affect the gradient, simplifying calculations.
Advanced Considerations
While the derivative of a constant is always zero, understanding the nuances is vital, especially when dealing with more complex scenarios:
-
Partial Derivatives: When dealing with functions of multiple variables, partial derivatives consider the rate of change with respect to only one variable while holding others constant. The partial derivative of a constant with respect to any variable is still zero.
-
Implicit Differentiation: When using implicit differentiation, even if a constant is implicitly involved in a function, its derivative remains zero.
-
Higher-Order Derivatives: The second derivative, third derivative, and so on, of a constant are all zero. This is because the derivative of zero (the first derivative of a constant) is zero, and the derivative of zero is zero, and so on.
-
Applications in Differential Equations: The property of a constant's derivative being zero is fundamental in solving differential equations. It often simplifies the equations and leads to solutions.
Conclusion
The seemingly simple statement, "the derivative of a constant is zero," underpins much of calculus and its various applications. Its understanding is fundamental for successfully navigating differentiation and interpreting the results in diverse contexts. This article has provided a comprehensive overview of the concept, its proof, implications, and practical applications, equipping you with a solid foundation to tackle more advanced calculus concepts. Remember, a firm grasp of this principle allows for efficient calculations, insightful interpretations, and a deeper understanding of the power of calculus in solving real-world problems. Through understanding this core principle, you become better equipped to tackle the complexities of calculus and leverage its power in various fields.
Latest Posts
Latest Posts
-
Does The Quotation Mark Go Before Or After A Period
May 13, 2025
-
A Dorsal Root Ganglion Contains Cell Bodies Of
May 13, 2025
-
Negative B Plus Or Minus The Square Root Of
May 13, 2025
-
All Parallelograms Have 4 Equal Sides
May 13, 2025
-
How Did The Wib Help America
May 13, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of A Constant Is 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.