Cos 2x 1 2 1 Cos2x
listenit
May 13, 2025 · 5 min read
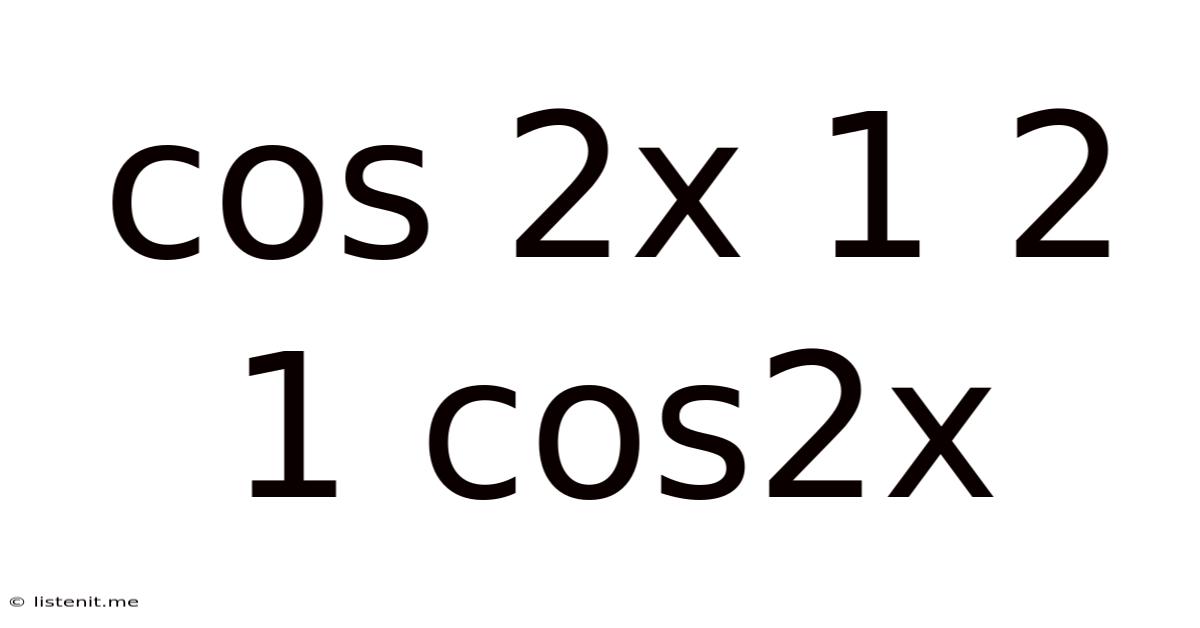
Table of Contents
Decoding the Trigonometric Identity: cos 2x = 1 - 2sin²x
The trigonometric identity cos 2x = 1 - 2sin²x is a fundamental equation in trigonometry, offering a powerful tool for simplifying expressions, solving equations, and understanding the relationships between different trigonometric functions. This article delves deep into this identity, exploring its derivation, applications, and connections to other trigonometric identities. We'll move beyond the mere statement of the identity to understand its true significance and practical utility.
Understanding the Double Angle Formula
The identity cos 2x = 1 - 2sin²x is a specific instance of the double angle formulas, which relate the trigonometric functions of an angle (2x) to the trigonometric functions of half that angle (x). These formulas are crucial for simplifying complex trigonometric expressions and solving trigonometric equations. They provide a bridge between angles and their doubled counterparts.
The double angle formula for cosine has three main forms:
- cos 2x = cos²x - sin²x (This is the most fundamental form)
- cos 2x = 1 - 2sin²x (Derived from the first form using the Pythagorean identity)
- cos 2x = 2cos²x - 1 (Also derived from the first form using the Pythagorean identity)
This article focuses on the second form: cos 2x = 1 - 2sin²x. We will explore its derivation and its various applications.
Derivation of cos 2x = 1 - 2sin²x
The derivation begins with the fundamental double angle formula for cosine: cos 2x = cos²x - sin²x. To arrive at the desired identity, we utilize the Pythagorean identity: sin²x + cos²x = 1. We can rearrange this to express cos²x as: cos²x = 1 - sin²x.
Now, substitute this expression for cos²x into the fundamental double angle formula:
cos 2x = (1 - sin²x) - sin²x
Simplifying this expression gives us the desired identity:
cos 2x = 1 - 2sin²x
This derivation clearly shows the direct relationship between the double angle formula and the Pythagorean identity, highlighting the interconnected nature of trigonometric identities.
Applications of the Identity: cos 2x = 1 - 2sin²x
The identity cos 2x = 1 - 2sin²x is incredibly versatile and finds applications in various areas, including:
-
Simplifying Trigonometric Expressions: This identity is particularly useful for simplifying expressions that involve both cosine and sine functions of a double angle. By replacing cos 2x with 1 - 2sin²x (or vice versa, depending on the context), you can often reduce the complexity of an expression, making it easier to analyze and manipulate.
-
Solving Trigonometric Equations: Many trigonometric equations can be solved more easily by applying this identity. By substituting 1 - 2sin²x for cos 2x, you can transform an equation into a simpler form that may be solvable using standard algebraic techniques. This often allows the isolation of a single trigonometric function, making the solution process more straightforward.
-
Calculus: This identity plays a crucial role in calculus, particularly in integration and differentiation of trigonometric functions. Replacing a complex trigonometric expression with a simpler equivalent using this identity can significantly simplify the integration or differentiation process.
-
Physics and Engineering: Trigonometric identities, including cos 2x = 1 - 2sin²x, are fundamental in various branches of physics and engineering, where they are used to model oscillatory and periodic phenomena. They are essential in analyzing waves, vibrations, and other cyclical processes.
Examples: Illustrating the Applications
Let's examine a few examples to see how this identity works in practice:
Example 1: Simplifying a Trigonometric Expression
Simplify the expression: 3cos 2x + 6sin²x
Using the identity cos 2x = 1 - 2sin²x, we substitute:
3(1 - 2sin²x) + 6sin²x = 3 - 6sin²x + 6sin²x = 3
The complex expression simplifies to a constant value of 3.
Example 2: Solving a Trigonometric Equation
Solve the equation: cos 2x = sin²x
Using the identity cos 2x = 1 - 2sin²x, we substitute:
1 - 2sin²x = sin²x
Adding 2sin²x to both sides:
1 = 3sin²x
Dividing by 3:
sin²x = 1/3
Taking the square root:
sinx = ±√(1/3)
This gives us two sets of solutions for x.
Example 3: Integration in Calculus
Consider the integral: ∫cos²x dx
We can use the identity cos 2x = 2cos²x - 1 to solve this:
cos²x = (cos 2x + 1) / 2
Therefore, the integral becomes:
∫(cos 2x + 1) / 2 dx = (1/2)∫(cos 2x + 1) dx = (1/4)sin 2x + (1/2)x + C where C is the constant of integration.
Connections to Other Trigonometric Identities
The identity cos 2x = 1 - 2sin²x is deeply intertwined with other fundamental trigonometric identities. Its derivation relies directly on the Pythagorean identity. Furthermore, it forms the basis for deriving other useful identities. For instance, by manipulating this identity, one can derive expressions for cos²x and sin²x in terms of cos 2x.
Conclusion: The Importance of cos 2x = 1 - 2sin²x
The trigonometric identity cos 2x = 1 - 2sin²x is far from just a mathematical curiosity. It’s a powerful tool with extensive applications across diverse fields. Understanding its derivation, its various forms, and its connections to other identities is fundamental to mastering trigonometry and its applications in higher-level mathematics, physics, engineering, and computer science. Its ability to simplify complex expressions, solve intricate equations, and facilitate smoother calculations makes it an invaluable asset in the arsenal of any mathematician or scientist. The examples provided in this article merely scratch the surface of its practical utility, highlighting the profound and pervasive influence of this seemingly simple yet remarkably powerful identity. Its continued relevance underscores its enduring importance in the realm of mathematics and beyond.
Latest Posts
Latest Posts
-
How Are Lactic Acid Fermentation And Alcoholic Fermentation Different
May 13, 2025
-
Is A Solution A Homogeneous Or Heterogeneous Mixture
May 13, 2025
-
Isotopes Of The Same Element Have The Same Number Of
May 13, 2025
-
What Is The Area Of Rhombus Abcd
May 13, 2025
-
How Many Electrons Does S 2 Have
May 13, 2025
Related Post
Thank you for visiting our website which covers about Cos 2x 1 2 1 Cos2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.