Common Multiple Of 7 And 9
listenit
Apr 06, 2025 · 5 min read
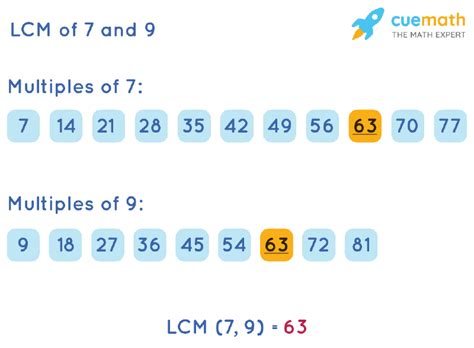
Table of Contents
Unveiling the Secrets of the Least Common Multiple of 7 and 9: A Deep Dive
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles unlocks a world of mathematical elegance and practical applications. This comprehensive guide delves into the intricacies of finding the LCM of 7 and 9, exploring various methods and highlighting the significance of this concept in diverse fields. We'll go beyond a simple answer, providing a robust understanding suitable for students, educators, and anyone fascinated by the beauty of mathematics.
Understanding Least Common Multiples (LCM)
Before we tackle the specific case of 7 and 9, let's establish a firm understanding of LCMs. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. It's a fundamental concept in number theory with wide-ranging applications in areas like:
- Fractions and Rational Numbers: Finding a common denominator when adding or subtracting fractions relies heavily on LCMs.
- Scheduling and Cyclical Events: LCMs are crucial in solving problems involving events that repeat at different intervals, such as determining when two machines operating at different frequencies will coincide.
- Modular Arithmetic: Used extensively in cryptography and computer science, modular arithmetic relies on the concept of LCM for various computations.
- Music Theory: The relationship between musical intervals and harmonies often involves LCMs.
Methods for Finding the LCM of 7 and 9
Several methods exist for determining the LCM of two numbers, each with its own advantages and suitability depending on the context. Let's explore the most common approaches:
1. Listing Multiples Method
This is a straightforward method, especially suitable for smaller numbers like 7 and 9. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, ...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, ...
Notice that the smallest multiple appearing in both lists is 63. Therefore, the LCM(7, 9) = 63.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical structure. We first find the prime factorization of each number:
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 9: 3 x 3 = 3²
Next, we identify the highest power of each prime factor present in either factorization:
- The highest power of 3 is 3²
- The highest power of 7 is 7¹
Finally, we multiply these highest powers together to obtain the LCM:
LCM(7, 9) = 3² x 7 = 9 x 7 = 63
This method is particularly valuable because it generalizes easily to finding the LCM of more than two numbers.
3. Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) of two numbers are intimately related. They satisfy the following equation:
LCM(a, b) x GCD(a, b) = a x b
Since 7 and 9 are relatively prime (they have no common factors other than 1), their GCD is 1. Therefore:
LCM(7, 9) = (7 x 9) / GCD(7, 9) = 63 / 1 = 63
This method is efficient when the GCD is easily determined, particularly when using the Euclidean algorithm for larger numbers.
Applications of LCM(7,9) = 63
The LCM of 7 and 9, being 63, finds practical application in various scenarios:
- Scheduling: Imagine two machines, one completing a cycle every 7 minutes and the other every 9 minutes. They will both be at the starting point of their cycles again after 63 minutes.
- Fraction Addition: To add fractions with denominators 7 and 9, we would find the least common denominator, which is 63. For example, 1/7 + 1/9 would become (9/63) + (7/63) = 16/63.
- Repeating Patterns: If two patterns repeat every 7 and 9 units respectively, their combined pattern will repeat every 63 units.
- Gear Ratios: In mechanical engineering, gear ratios and their synchronization often involve finding LCMs to determine when gears will align perfectly.
Beyond the Basics: Extending the Concept
While we've focused on finding the LCM of 7 and 9, the principles discussed apply broadly. Understanding the underlying mathematical concepts allows us to tackle more complex problems:
- LCM of more than two numbers: The prime factorization method extends seamlessly to finding the LCM of three or more numbers. Simply find the prime factorization of each number, identify the highest power of each prime factor, and multiply them together.
- LCM and fractions with more than two denominators: When adding or subtracting fractions with multiple denominators, find the LCM of all the denominators to determine the common denominator.
- Applications in abstract algebra: The concepts of LCM and GCD play a fundamental role in abstract algebra, particularly in ring theory and ideal theory.
Conclusion: The Enduring Significance of LCMs
The seemingly simple task of finding the least common multiple of 7 and 9 reveals a wealth of mathematical depth and practical utility. Mastering different methods for calculating LCMs empowers us to solve a broad range of problems across various disciplines, from simplifying fractions to scheduling complex events. By understanding the underlying principles, we unlock a deeper appreciation for the elegance and power of number theory and its pervasive influence on our world. The seemingly small number 63, representing the LCM of 7 and 9, serves as a testament to the interconnectedness and beauty of mathematics. This exploration should inspire further investigation into the fascinating world of number theory and its many applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about Common Multiple Of 7 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.