Change In X Over Change In Y
listenit
May 09, 2025 · 6 min read
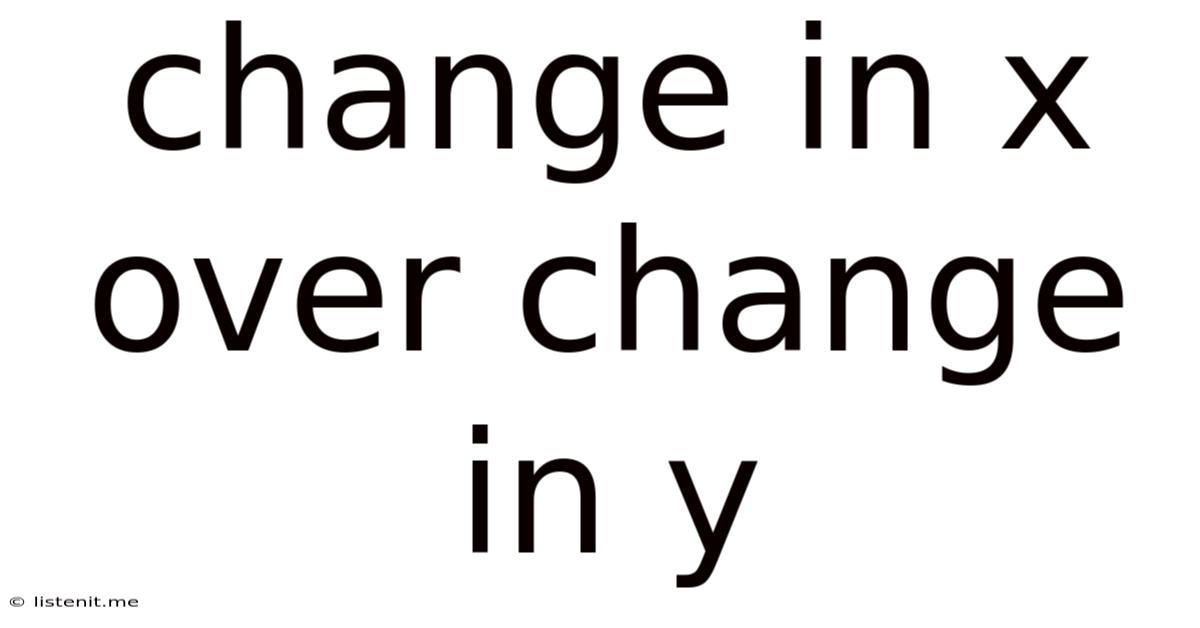
Table of Contents
Understanding Change in X Over Change in Y: A Deep Dive into Rates of Change
The concept of "change in x over change in y" might sound intimidating, but it's a fundamental building block in mathematics and various scientific fields. More formally known as the rate of change, or in its most common application, the slope, understanding this concept is crucial for interpreting data, predicting trends, and solving real-world problems. This comprehensive guide will explore this concept in depth, covering its applications, calculations, and interpretations.
What Does "Change in X Over Change in Y" Mean?
At its core, "change in x over change in y" represents the ratio of the change in one variable (x) to the change in another variable (y). It quantifies how much y changes for every unit change in x. The familiar slope of a line is a perfect example. When we have a straight line on a graph, the slope tells us the steepness of that line, revealing how much the y-value changes for each unit increase in the x-value.
The Importance of Context
The interpretation of "change in x over change in y" is heavily reliant on the context. The variables x and y represent different things depending on the situation. For instance:
-
In physics: x could represent time (t) and y could represent distance (d). The "change in x over change in y" (Δd/Δt) would then be the velocity – the rate of change of distance with respect to time.
-
In economics: x could represent quantity of goods and y could represent price. The "change in x over change in y" (Δp/Δq) represents the price elasticity of demand, indicating the responsiveness of demand to price changes.
-
In finance: x could represent time and y could represent the value of an investment. The "change in x over change in y" represents the rate of return on the investment.
-
In data analysis: x and y could represent any two variables you're studying. Calculating the "change in x over change in y" helps reveal the correlation between them.
Calculating Change in X Over Change in Y
The calculation is straightforward:
Change in X over Change in Y = (Change in X) / (Change in Y) = Δx / Δy
Where:
- Δx represents the change in x (x₂ - x₁), where x₂ is the final value of x and x₁ is the initial value of x.
- Δy represents the change in y (y₂ - y₁), where y₂ is the final value of y and y₁ is the initial value of y.
Important Note: The order of x and y matters! The formula above calculates the change in x over the change in y. If you need to calculate the change in y over the change in x (which is more common), simply switch the numerator and the denominator.
Example Calculation:
Let's say we're tracking the growth of a plant. At time t₁ = 1 week, the plant's height h₁ = 2 cm. At time t₂ = 3 weeks, the plant's height h₂ = 6 cm.
To find the rate of growth (change in height over change in time):
Δh / Δt = (h₂ - h₁) / (t₂ - t₁) = (6 cm - 2 cm) / (3 weeks - 1 week) = 4 cm / 2 weeks = 2 cm/week
This tells us the plant grows at a rate of 2 centimeters per week.
Understanding the Slope of a Line
The "change in x over change in y" is most readily visualized as the slope of a line. In the equation of a line (y = mx + c), 'm' represents the slope. The slope is a measure of the steepness of the line and its direction.
-
Positive Slope: A positive slope indicates a positive relationship between x and y. As x increases, y increases. The line slopes upwards from left to right.
-
Negative Slope: A negative slope indicates a negative relationship between x and y. As x increases, y decreases. The line slopes downwards from left to right.
-
Zero Slope: A zero slope indicates that y does not change regardless of the changes in x. The line is horizontal.
-
Undefined Slope: An undefined slope occurs when the change in x is zero (vertical line). This means there's an infinite change in y for a zero change in x.
Calculating Slope from Two Points
Given two points (x₁, y₁) and (x₂, y₂), the slope (m) can be calculated as:
m = (y₂ - y₁) / (x₂ - x₁)
This is essentially the same as the "change in y over change in x" formula.
Applications Across Disciplines
The concept of "change in x over change in y" or its inverse, finds broad application in various fields:
1. Physics: Velocity and Acceleration
-
Velocity: As mentioned earlier, velocity is the rate of change of displacement (distance) with respect to time. A positive velocity indicates movement in a specific direction, while a negative velocity suggests movement in the opposite direction.
-
Acceleration: Acceleration is the rate of change of velocity with respect to time. A positive acceleration signifies increasing speed, and a negative acceleration (deceleration) represents decreasing speed.
2. Calculus: Derivatives
In calculus, the concept extends to the derivative, which represents the instantaneous rate of change of a function at a specific point. The derivative is a fundamental tool for analyzing the behavior of functions, finding extrema (maximum and minimum values), and solving optimization problems.
3. Economics: Elasticity
-
Price Elasticity of Demand: This measures the responsiveness of the quantity demanded of a good or service to a change in its price. A high elasticity suggests that demand is highly sensitive to price changes, while a low elasticity indicates that demand is less sensitive.
-
Income Elasticity of Demand: This measures how much demand changes in response to a change in consumer income.
4. Finance: Rate of Return
The rate of return on an investment is calculated as the change in the investment's value over the change in time. This metric is crucial for evaluating the performance of investments and comparing different investment options.
5. Data Analysis and Statistics: Correlation and Regression
-
Correlation: The "change in x over change in y" can help assess the correlation between two variables. A strong correlation indicates a close relationship between them, while a weak correlation suggests a weaker relationship.
-
Regression Analysis: Regression analysis uses the concept of slope to model the relationship between variables and make predictions. The slope of the regression line indicates the strength and direction of the relationship.
Beyond Linear Relationships
While the "change in x over change in y" is straightforward for linear relationships (straight lines), it becomes more complex for non-linear relationships (curves). For curves, the rate of change is not constant; it varies at different points along the curve. This is where calculus becomes indispensable, allowing us to calculate the instantaneous rate of change at any point using derivatives.
Conclusion: A Versatile Tool for Understanding Change
The seemingly simple concept of "change in x over change in y" underpins many critical calculations and analyses across various scientific and mathematical disciplines. Understanding this concept, along with its application in calculating slopes, rates of change, and derivatives, is fundamental to interpreting data, modeling relationships between variables, and predicting future trends. Whether you're analyzing physical phenomena, economic trends, or financial investments, mastering this concept is a significant step towards a deeper understanding of the world around us. Its versatility and importance should not be underestimated.
Latest Posts
Latest Posts
-
Decomposers Are Necessary In An Ecosystem Because They
May 10, 2025
-
Which Color Has The Least Energy
May 10, 2025
-
Is Saturn A Gas Giant Or A Terrestrial Planet
May 10, 2025
-
What Is The Completely Factored Form Of X3 64x
May 10, 2025
-
The Transparent Part Of The Eye Is The
May 10, 2025
Related Post
Thank you for visiting our website which covers about Change In X Over Change In Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.