Ax By C Solve For X
listenit
May 09, 2025 · 5 min read
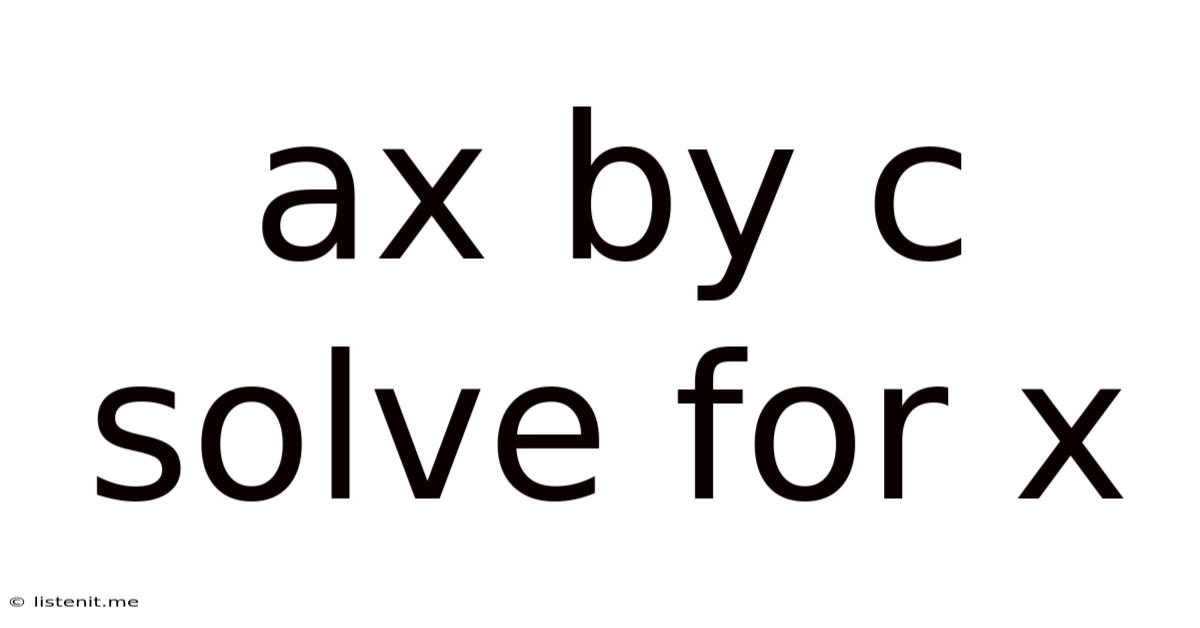
Table of Contents
Solving for x: A Comprehensive Guide to Ax = C
Solving algebraic equations is a fundamental skill in mathematics, forming the bedrock for more advanced concepts. One of the most basic, yet crucial, equations is the simple linear equation Ax = C, where A and C are constants, and x is the variable we aim to solve for. This seemingly straightforward equation provides a solid foundation for understanding more complex algebraic manipulations. This article will comprehensively explore the process of solving for x in Ax = C, covering various scenarios, offering practical examples, and highlighting common pitfalls to avoid.
Understanding the Equation Ax = C
Before diving into the solution, let's unpack the meaning of Ax = C. This equation represents a linear relationship between two variables, x and a constant multiple of x (Ax). The constant A acts as a scaling factor for x, while C represents the result of this scaling. Our goal is to isolate x, leaving it on one side of the equation by itself.
Key Terms:
- Variable (x): The unknown value we are trying to find.
- Constants (A and C): Known numerical values. A cannot be zero (we'll explore why later).
- Coefficient (A): The number multiplying the variable x.
- Equation: A mathematical statement asserting the equality of two expressions.
Solving for x: The Fundamental Approach
The core principle behind solving Ax = C involves performing the same operation on both sides of the equation to maintain balance. The inverse operation of multiplication (which is what connects A and x) is division. Therefore, to isolate x, we divide both sides of the equation by A:
(Ax)/A = C/A
This simplifies to:
x = C/A
This is the general solution for x in the equation Ax = C.
Illustrative Examples: Putting the Solution into Practice
Let's solidify our understanding with some concrete examples:
Example 1: Simple Solution
Solve for x in the equation 5x = 25.
Here, A = 5 and C = 25. Applying the formula:
x = C/A = 25/5 = 5
Therefore, x = 5.
Example 2: Involving Negative Numbers
Solve for x in the equation -3x = 12.
Here, A = -3 and C = 12. Applying the formula:
x = C/A = 12/(-3) = -4
Therefore, x = -4. Notice how the negative coefficient of x affects the sign of the solution.
Example 3: Fractional Coefficients
Solve for x in the equation (1/2)x = 7.
Here, A = 1/2 and C = 7. Applying the formula:
x = C/A = 7 / (1/2) = 7 * 2 = 14
Therefore, x = 14. Remember that dividing by a fraction is equivalent to multiplying by its reciprocal.
Example 4: Decimal Coefficients
Solve for x in the equation 2.5x = 10.
Here, A = 2.5 and C = 10. Applying the formula:
x = C/A = 10 / 2.5 = 4
Therefore, x = 4. This demonstrates that the method works equally well with decimal coefficients.
Handling Special Cases: Zero and Undefined Solutions
While the formula x = C/A works beautifully in most cases, we need to address two special scenarios:
1. When A = 0:
If A = 0, the equation becomes 0x = C. This presents two possibilities:
- If C = 0: Then the equation 0x = 0 is true for any value of x. In this case, there are infinitely many solutions.
- If C ≠ 0: Then the equation 0x = C (where C is any non-zero number) has no solution. There is no value of x that can satisfy this equation.
2. When A and C are both 0:
If both A and C are 0, the equation becomes 0x = 0. This equation is true for any value of x. Thus, there are infinitely many solutions.
These special cases highlight the importance of considering the values of A and C before applying the standard solution.
Practical Applications of Solving Ax = C
The seemingly simple equation Ax = C finds applications in various fields:
- Physics: Calculating velocities, accelerations, and forces.
- Engineering: Determining dimensions, stresses, and strains in structures.
- Finance: Computing interest, returns on investments, and loan payments.
- Chemistry: Calculating molar concentrations and reaction rates.
- Computer Science: Solving linear systems in algorithms and simulations.
Expanding the Scope: More Complex Equations
While Ax = C is a foundational equation, it lays the groundwork for solving more intricate algebraic equations. Understanding this basic concept is essential for tackling problems involving multiple variables, exponents, and other mathematical operations.
For instance, consider an equation like 2x + 5 = 11. While seemingly more complex, solving it still relies on the fundamental principles of performing the same operation on both sides of the equation to isolate x. First, you would subtract 5 from both sides, resulting in 2x = 6. Then, you would use the method described above to solve for x (x = 6/2 = 3).
Troubleshooting Common Mistakes
Several common pitfalls can hinder accurate solutions:
- Incorrect order of operations: Always follow the order of operations (PEMDAS/BODMAS) carefully.
- Sign errors: Pay close attention to the signs of the numbers, especially when dealing with negative numbers.
- Fractional arithmetic errors: Master the rules of fraction arithmetic, including multiplying and dividing fractions.
- Forgetting to perform operations on both sides: Remember, any operation performed on one side of the equation must also be performed on the other side to maintain equality.
Conclusion: Mastering the Fundamentals
Solving Ax = C, while simple in its form, underpins a deeper understanding of algebraic manipulation. Mastering this foundational equation empowers you to approach more complex problems with confidence. Through consistent practice and attention to detail, you can develop proficiency in solving for x and unlock the doors to more advanced mathematical concepts. Remember to check your answers and understand the underlying principles, not just the rote application of the formula. This ensures a strong mathematical foundation for future endeavors.
Latest Posts
Latest Posts
-
Find The Quotient And Remainder Using Synthetic Division
May 09, 2025
-
The Basic Units Of All Living Things Are
May 09, 2025
-
Simplify 2 3 2 8 2
May 09, 2025
-
9 Is 50 Of What Number
May 09, 2025
-
Why Is Ethanol Soluble In Water
May 09, 2025
Related Post
Thank you for visiting our website which covers about Ax By C Solve For X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.